Number Of Multiplications And Additions In Matrix Multiplication
Computing element a_ij of AB requires taking the dot product of row i in A and column j in B. We call the number 2 in this case a scalar so this is known asscalar multiplication.
Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
A matrix is a rectangular array of numbers or other mathematical objects for which operations such as addition and multiplication are defined.
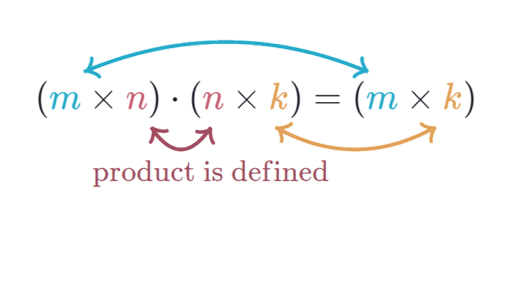
Number of multiplications and additions in matrix multiplication. In general multipling two matrices of size N X N takes N3 operations. It is also read as 3 by 3 or 2 by 2 etc. The left column represents 2x2 matrix multiplication.
Each of the other columns represents a single one of the 7 multiplications in the algorithm and the sum of the columns. For multiplying the two 22 dimension matrices Strassens used some formulas in which there are seven multiplication and eighteen addition subtraction and in brute force algorithm there is eight multiplication and four addition. 2 1 2.
Definition of Multiplication of Matrix. This definition of a. Thus the total number of operations is n2nn-12n3-n2 On3.
Int f int x x_3 x x x. If A is the matrix m x r and B is a matrix r x n then the product of AB is the matrix m x n whose entries are determined as follows. Of Rows into Noof Columns.
The result is a 4x1 matrix computed using 16 multiplications. May 17 2020 Matrix related programs are famous in interview which not only check the knowledge of programming but checks the basic idea of mathematics. The Formula of order of a Matrix mnhere m is use to represent No.
Since this savings in the number of multiplications was achieved at the expense of making extra additions we must check the number of additions An made by Strassens algorithm. Addition and Subtraction operation takes less time compared to multiplication. To search for entries in row i and column i of AB select row i from matrix A and column j from matrix B.
Image to be added soon Here are the calculations. To multiply a matrix by a single number is a very easy and simple task to do. To multiply two matrices of order n 1 the algorithm needs to multiply seven matrices of order n 2 and make 18 additionssubtractions of matrices of size n 2.
X_12 x_6 x_6 x_24 x_12 x_12 return x_24 x_6 This. We will describe an algorithm discovered by VStrassen and usually called Strassens Algorithm that allows us to multiply two n by n matrices A and B with a number of multiplications and additions which is a small multiple of n ln 7 ln 2 when n is of the form 2 k. Matrix Multiplication is one of the most fundamental operation in Machine Learning and optimizing it is the key to several optimizations.
2 4 8. The main idea is due to Winograd it can be found in Stothers thesis for istance. It is possible to multiply two 4 4 matrix A B with only 48 multiplications.
According to Wikipedia. The order of a Matrix is just tells that how many rows and columns are exits in this Matrix. Naïve matrix multiplication requires one multiplication for each 1 of the left column.
Computing the dot product requires n multiplications and n-1 additions. Volker Strassen first published his algorithm in 1969. Since then we have come a long way to better and clever matrix multiplication algorithms.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. Multiply the corresponding entries from the rows and columns together and then add the resulting multiplication. So the question is asking what is the minimum number of multiplications possible.
2 0 0. Java Program Matrix Addition Subtraction Multiplication Transpose Posted By. A i x 1 x 2 x 3 x 4.
For any row A i x 1 x 2 x 3 x 4 of A let A i be the ausiliary quantity. Next multiply P with this matrix to get the answer in 8421 multiplications. Since there are n2 elements the dot product must be computed n2 times.
Of Rows and n is No. When n 1 no additions are made since two. 2 -9 -18.
Here is 6 multiplications and likely the interviewers ideal solution. X_6 x_3 x_3. This is like 2 28 instead of 23.
Multiply Q and R to get a 2x1 matrix in 8241 multiplications. Unlike a simple divide and conquer method which uses 8 multiplications and 4 additions Strassens algorithm uses 7 multiplications which reduces the time complexity of the matrix multiplication algorithm a little bit. We dont multiply the No.
The utility of Strassens formula is shown by its asymptotic superiority when order n of matrix reaches infinity.
Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
Matrix Multiplication Dimensions Article Khan Academy
Matrix Multiplication Inches Closer To Mythic Goal Techthoroughfare
Matrix Multiplication Verification Mathematics Stack Exchange
4 Multiplication Of Matrices
3 4a Matrix Operations Finite Math
Solved A Assume The Matrix Multiplication Of Figure 16 6 Require Chegg Com
Assignment Of Computation In Matrix Multiplication Download Scientific Diagram
3 4a Matrix Operations Finite Math
Divide And Conquer Set 5 Strassen S Matrix Multiplication Tutorialspoint Dev
Engineering Mathematics On The Go 19 Operations With Matrices Ad Mathematics Matrix Multiplication Matrix
Gabriel Peyre On Twitter Strassen Algorithm Reduces The Complexity Of Matrix Multiplication In Term Of Number Of Multiplications Https T Co 2lijbdqyh0 Https T Co X3r9ul9kfr
Inverse Matrix Matrix Multiplication Youtube
Video 27 Number Of Additions And Multiplications In Matrix Product Gate Cs Youtube
Introduction To Matrices And Matrix Arithmetic For Machine Learning
Pin On Algebra
3 4a Matrix Operations Finite Math
Properties Of Matrix Multiplication Article Khan Academy
Multiplying Matrices Article Matrices Khan Academy
