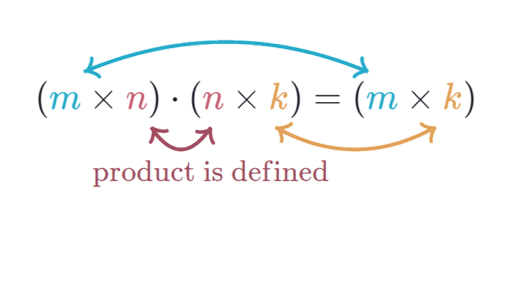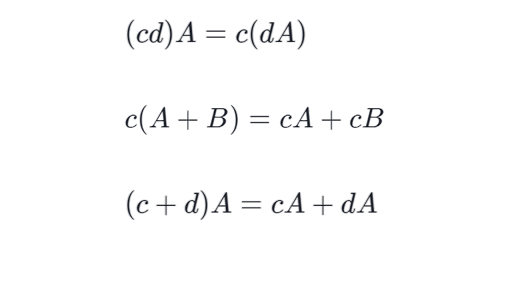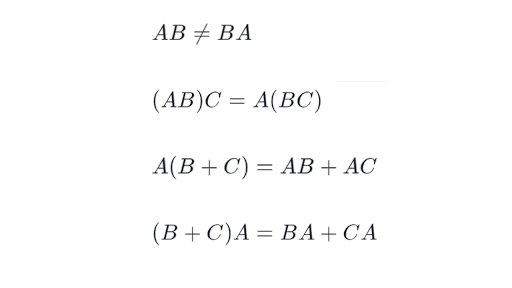Matrix Dot Product Properties

M2 It is positive non-degenerate. Recall from above that the dot product of any two different rows or columns of a rotation matrix is zero while the dot product of any row or column with itself is one.

Vector Inner Product Sharetechnote

It is linear in each variable This means that if and are scalars h x yzi hxzi hyzi.

Matrix dot product properties. Dot Product and Matrix Multiplication DEFp. These properties are extremely important though they are a little boring to prove. In mathematics particularly in linear algebra matrix multiplication is a binary operation that produces a matrix from two matrices.

Then for x 2Rn and y 2Rm. The length or norm of a vectora2Rd is defined by kakaa12 q a2 1 a2 d. Note that the dot product of two vectors is a scalar.

18 If A aijis an m n matrix and B bijis an n p matrix then the product of A and B is the m p matrix C cijsuch that. This and other properties of the dot product are stated below. Uv v u su v suv usv uv w uv uw 0u 0 uu kuk2 where kuk.

M3 It satisfies the triangle inequality for metrics. Review of Dot Product For vectorsab2Rd we define the dot product by aba 1b 1 a db d. Heres just a few properties of dot products which I will not prove at this time.

We are now ready to define matrix product. Example 1 Compute the dot product for each of the following. 0 0 0 v 2 v.

Definition Let be a matrix and a matrix. The dot product satis es these three properties. CAT is a subspace of.

In Euclidean geometry the dot product of the Cartesian coordinates of two vectors is widely used. You end up 18 53 8 4 14 40 13 2 15 and 69 so our product AB this matrix2224. The rst two properties can be checked by direct computation.

So the i dot product ii Euclidean. M1 It is symmetric. Let Abe an m nmatrix.

Here is the dot product of vectors. U v 0 when u and v are orthogonal. Computing Matrix-Vector Products Dot Product Properties Let uvw be arbitrary vectors in Rn and s 2R any real scalar.

Dot product of vectors and matrices matrix multiplication is one of the most important operations in deep learning. For this reason the dot product is sometimes called a scalar product. Au bv w au w bv w where a and b are scalars Here is the list of properties of the dot product.

For any x we have hxxi 0. Then their product is a matrix whose -th entry is equal to the dot product between the -th row of and the -th column of for and. Again this distance function - or metric - satisfies three basic properties which are direct consequences of the ones above.

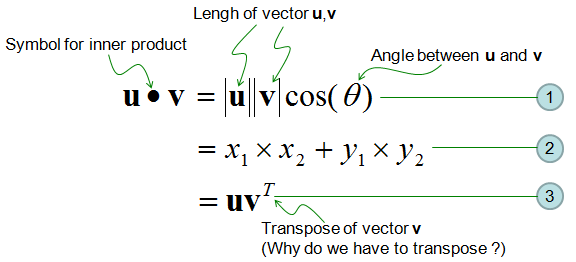
For matrix multiplication the number of columns in the first matrix must be equal to the number of rows in the second matrix. U v uv cos θ. The dot product is also an example of an inner product and so on occasion you may hear it called an inner product.

Dot Product of a matrix and a vector Unlike addition or subtraction the product of two matrices is not calculated by multiplying each cell of one matrix with the corresponding cell of the other but we calculate the sum of products of rows of one matrix with the column of the other matrix as shown in the image below. A b a1b1 a2b2 a3b3 1 1 a b a 1 b 1 a 2 b 2 a 3 b 3 Sometimes the dot product is called the scalar product. Extended Example Let Abe a 5 3 matrix so A.

U v v u. Is 0 if and only if A0. U a1anand v b1bnis u 6 v a1b1 anbn regardless of whether the vectors are written as rows or columns.

A1 a2 b1 b2 a1b1 a2b2 y nparray123 x nparray234 npdotyx 20. The only way it can be zero is if x0. Algebraic Properties of the Dot Product.

This can be written in matrix and tensor notation as R RT I and RikRjk δij R R T I and R i k R j k δ i j. In words the order of multiplication doesnt matter. Certain basic propertiesfollow immediately from the definition.

1 Commutative Property For any two vectors A and B A. Another property of the dot product is. The first thing to notice is that the dot product of two vectors gives us anumber.

It is often called the inner product of Euclidean space even though it is not the only inner product that can be defined on Euclidean space. Properties of the Dot Product. Well you take the first row dot product of the second column 3 times 0 is 0 5 times 1 is 5 so you end you with 5 then you keep going2214.

For any vectorsab andc and any real number a bba. In other words. In other words the -th entry of is.

It is symmetric which means that hxyi hyxi. A quick examination of Example exdotex will convince you that the dot product is commutative. NA is a subspace of CA is a subspace of The transpose AT is a matrix so AT.

The product of matrices A and B is denoted as AB. Here is the proof of the statemengt that the dot product of n-vectors satisfies the following properties. Is greater than or equal to 0.

Where theory is concerned the key property of transposes is the following. The dot product of two vectors is a scalar. Ax y xATy.

2 Scalar Multiplication Property For any two vectors A and B and any real number c cA. In mathematics the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number. It takes a second look to see that anything is going on at all but look twice or 3 times.

Notice that the dot product of vectors can be viewed as the product of matrices. Notice 8 times B is defined if I did. The resulting matrix known as the matrix product has the number of rows of the first and the number of columns of the second matrix.

17 The dot product of n-vectors. There holds ab a b Cauchy-Schwarz inequality ab a b triangle inequality If we denote the angle between nonzero vectorsab by q there holds ab a b cosq. X yi hzxi hzxi.

Algebraically the dot product is the sum of the products. Properties of Dot Product.

Matrix Algebra

Scalar And Vector Triple Product Youtube

Inner Dot Product Of Two Vectors Applications In Machine Learning

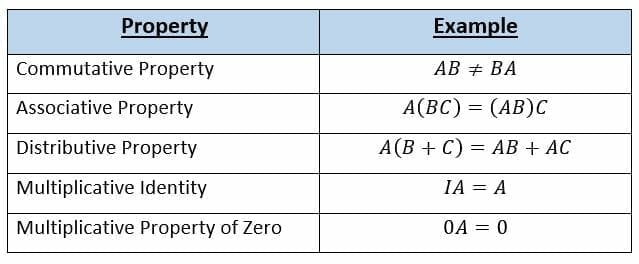
Matrix Multiplication Explanation Examples

Matrix Algebra

Lesson Video Properties Of Determinants Nagwa

Associative Property Of Matrix Multiplication Video Khan Academy

Matrix Multiplication Dimensions Article Khan Academy

Geometry Of R2 And R3 Dot And Cross Products Ppt Download

Part 23 Orthonormal Vectors Orthogonal Matrices And Hadamard Matrix By Avnish Linear Algebra Medium

Cross Product For Calculus Everything You Need To Know

Inner Dot Product Of Two Vectors Applications In Machine Learning

What Properties Must An Operation Satisfy In Order To Be Classified As A Product For Example What Does The Dot Product Have In Common With The Cross Product Quora

Chapter 4 Euclidean Vector Spaces Ppt Video Online Download

What Properties Must An Operation Satisfy In Order To Be Classified As A Product For Example What Does The Dot Product Have In Common With The Cross Product Quora

Properties Of Matrix Scalar Multiplication Article Khan Academy

Chap 2 Matrices 2 1 Operations With Matrices Ppt Video Online Download

Properties Of Matrix Multiplication Article Khan Academy

Inner Dot Product Of Two Vectors Applications In Machine Learning