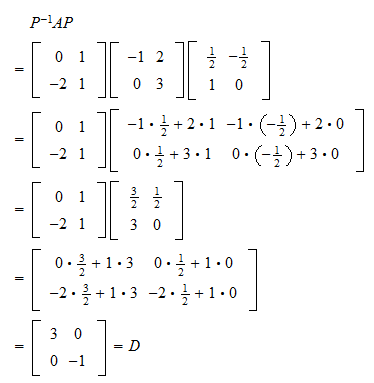Matrix Diagonalization Condition

19 Sep, 2021

608Diagonal matrices CAN have zeros along the main diagonal. D B 1 A B well.

Show That This Matrix Is Not Diagonalizable Mathematics Stack Exchange

Now that we know about eigenvalues and eigenvectors we are ready to learn about diagonalization.

Matrix diagonalization condition. The matrix is diagonalizabel if and only if the sum of these dimensions is n. An n matrix is diagonalizable if the sum of the eigenspace dimensions is equal to n. Hermit matrix-matrix which is equal to their conjugate transponse-is normal so diagonalizable.

If the calculator did not compute something or you have identified an error or you have a suggestionfeedback please write it in the comments below. Put in another way a matrix is diagonalizable if andonly if all of its elementary divisors are linear The following sufficient but not necessary condition is often useful. A is diagonalizable if and only if its minimal polynomial can be factored into a product of linear factors without passing to an extension field with no repeated roots.

An n n matrix A is diagonalizable if it is similar to a diagonal matrix. That is if there exists an invertible n n matrix C and a diagonal matrix D such that A CDC 1. Otherwise compute the dimension of each eigenspace.

The matrix joint block diagonalization problem jbdp of a given matrix set A A im i1 is about ﬁnding a nonsingular matrix W such that all W TA iW are block diagonal. Find the eigenvalues of the matrix and determine whether there is a sufficient number to guarantee that the matrix is diagonalizable. There is a simple sufficient condition for diagonalizability.

We now know that an matrix is diagonalizable if and only if has linearly independent eigenvectors. Recall that the matrix may be diagonalizable even though it is not guaranteed to be diagonalizable by. In particular for real matrices that means its minimal polynomial has only real roots and no repeated roots.

Generically such a matrix W may not. Orthogonal matrix-real symmetric matrix- is Hermit matrix so diagonalizable. The diagonalization theorem states that an matrix is diagonalizable if and only if has linearly independent eigenvectors ie if the matrix rank of the matrix formed by the eigenvectors is.

Normal matrices-those which commutate with its hermit matrix- are diagonalizable. If is large checking for linear independence can be tedious. In this section you will look at another classic problem in linear algebra called the diagonalization problem.

Sufficient Condition for Diagonalization If an nx n matrix A has n distinct eigenvalues then the. A linear map of T. A matrix is diagonalizable by a unitary matrix if and only if it is a normal matrix.

Condition numbers can also be defined for nonlinear functions and can be computed using calculus. The calculator will diagonalize the given matrix with steps shown. By using this website you agree to our Cookie Policy.

If a n n matrix has n distinct eigenvalues then it is automatically diagonalizable. The problem is this. Definition of Diagonalizable Matrix.

Matrices that are similar to diagonal matrices are called diagonalizable. A matrix that is not invertible has condition number equal to infinity. A diagonalizable matrix is any square matrix or linear map where it is possible to sum the eigenspaces to create a corresponding diagonal matrix.

A matrix or linear map is diagonalizable over the field F if and only if its minimalpolynomial is a product of distinct linear factors over F. Size of the matrix. This involves writing a matrix as a product of other matric.

V V is diagonalizable if the sum of eigenspace dimensions is equal to dim V. Given two diagonalizable matrices they commute if and only if they can be diagonalized simultaneously that is if they share the same orthonormal basis of eigenvectors. A matrix is diagonal when all entries NOT on th.

I kind of misspoke at 035. Concerning the sentence There exists a matrix B and a diagonal matrix D such that. Free Matrix Diagonalization calculator - diagonalize matrices step-by-step This website uses cookies to ensure you get the best experience.

Skip to the 4 ways. Practically such a matrix is almost singular and the computation of its inverse or solution of a linear system of equations is prone to large numerical errors. It includes the matrix joint diagonalization problem jdp as a special case for which all WTA iW are required diagonal.

Eigenvalues And Eigenvectors Ppt Video Online Download