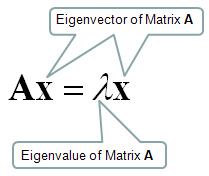Eigenvalues And Matrix Multiplication Relationship
The same result is true for lower triangular matrices. I think you can get bounds on the modulus of the eigenvalues of the product.
1 then v is an eigenvector of the linear transformation A and the scale factor λ is the eigenvalue corresponding to that eigenvector.

Eigenvalues and matrix multiplication relationship. Not an expert on linear algebra but anyway. For any triangular matrix the eigenvalues are equal to the entries on the main diagonal. EIGENVALUES OF THE LAPLACIAN AND THEIR RELATIONSHIP TO THE CONNECTEDNESS OF A GRAPH3 27 UTAU 10 k 0 k 1 A 2 A 2 2M kR so by inductive hypothesis there exists an orthogonal matrix Cwhose columns form an orthonormal basis of eigenvectors of A.
Some students are puzzled as to why the eigenvalues of a matrix would have any particular relationship to a power spectrum which seems a disconnected concept. These eigenvalues can in general be complex even if all entries of are real. The algebraic multiplicity of an eigenvalue is the number of times it appears as a root of the characteristic polynomial ie the polynomial whose roots are the eigenvalues of a matrix.
The geometric multiplicity of an eigenvalue is the dimension of the linear space of its associated eigenvectors ie its eigenspace. Rn to Rn x λx. The diagonal elements of a triangular matrix are equal to its eigenvalues.
To find the eigenvectors of a triangular matrix we use the usual procedure. Almost all vectors change di-rection when they are multiplied by A. The Relationship between Hadamard and.
Viewed as a linear transformation from A sends vector to a scalar multiple of itself. If is an eigenvector of the transpose it satisfies By transposing both sides of the equation we get. Equation 1 is the eigenvalue equation for the matrix A.
First we look at the relationship between matrix-vector multiplication and eigenvalues. A100 was found by using the eigenvalues of A not by multiplying 100 matrices. If Ax λx for some scalar λ and some nonzero vector xx then we say λ is an eigenvalue of A and x is an eigenvector associated with λ.
So to take advantage of the simplification we like to. Stack Exchange network consists of 177 QA communities including Stack Overflow the largest most trusted online community for developers to learn share. The row vector is called a left eigenvector of.
To explain eigenvalues we first explain eigenvectors. Those eigenvalues here they are 1 and 12 are a new way to see into the heart of a matrix. While conventional matrix multiplication is indicated as usual by juxtaposi-.
Eigenvalues and eigenvectors Introduction to eigenvalues Let A be an n x n matrix. Eigenvalues of a triangular matrix. For the n-by-n square matrix there are eigenvectors and corresponding scalar eigenvalues.
Equation 1 can be stated equivalently as A λ I v 0 displaystyle leftA-lambda Irightmathbf v mathbf 0 2 where I is the n by n identity matrix and 0 is the zero vector. In the following pages when we talk about finding the eigenvalues and eigen-vectors of some nnmatrix A what we mean is that Ais the matrix representa-tion with respect to the standard basis in Rn of a linear transformation L and the eigenvalues and eigenvectors of Aare just the eigenvalues and eigenvectors of L. I believe there is also a discussion about the relationship between the complexities of eigenvalues and matrix multiplication in the older Aho Hopcroft and Ullman book The Design and Analysis of Computer Algorithms however I dont have the book in front of me and I.
The power of this relationship is that when and only when we multiply a matrix by one of its eigenvectors then in a simplified equation we can replace a matrix with just a simple scalar value. Even if and have the same eigenvalues they do not necessarily have the same eigenvectors. There are very short 1 or 2 line proofs based on considering scalars xAy where x and y are column vectors and prime is transpose that real symmetric matrices have real eigenvalues and that the eigenspaces corresponding to distinct eigenvalues are orthogonal.
For an n-by-n matrix A all of whose eigenvalues are real denote the algebraically smallest of these eigenvalues by X J A and the largest by XA. In the next section we explore an important process involving the eigenvalues and eigenvectors of a matrix. The distribution of the eigenvalues of an autocorrelation matrix approach the power spectrum asymptotically as the order of the matrix increases this is known as Szegös theorem1 12.
We now examine some further properties of eigenvalues and eigenvectors to set up the central idea of singular value decompositions in Section 182 below. Certain exceptional vectors x are in the same.
Explained Matrices Mit News Massachusetts Institute Of Technology

Part 22 Eigenvalues And Eigenvectors By Avnish Linear Algebra Medium
What Are The Conditions Necessary For Matrix Multiplication Quora

Eigenvalues Eigenvectors Definition Equation Examples Video Lesson Transcript Study Com
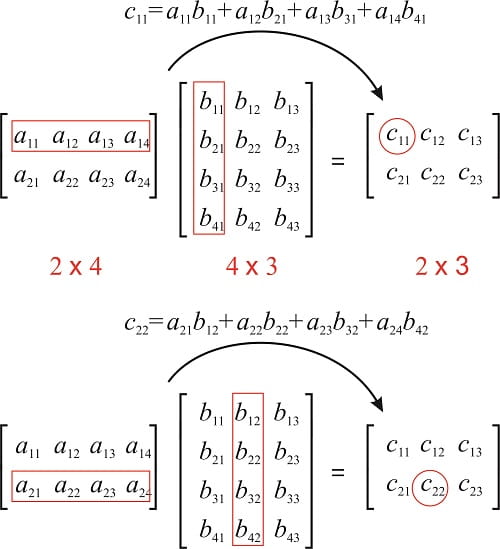
02 00 Linear Algebra Ipynb Colaboratory

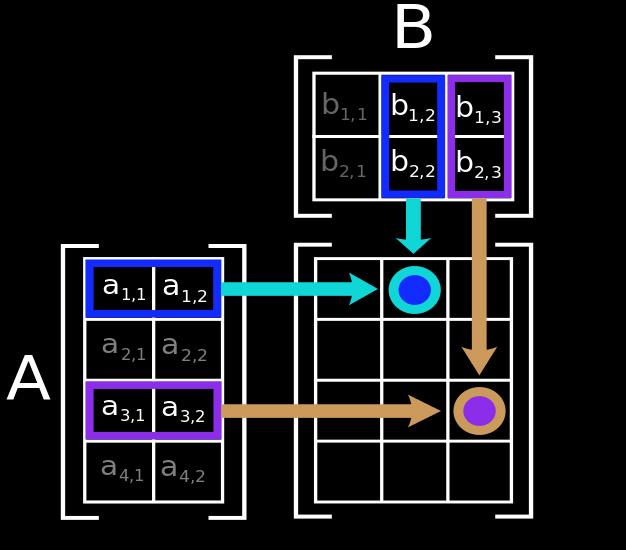
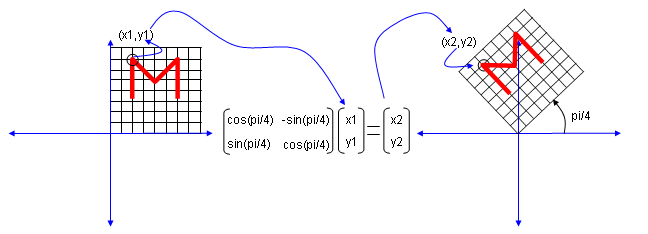
What Is The Intuition Behind Multiplication Of Matrices Quora

Eigenvalue Of Matrix Determinant Equals To The Product Of All Its Eigenvalue Mathematics Stack Exchange

Eigenvalue Feature 4 The Trace Youtube
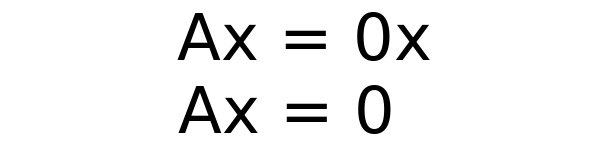
Part 22 Eigenvalues And Eigenvectors By Avnish Linear Algebra Medium

Why Is Matrix Multiplication Defined The Way It Is Quora

Multiplication Of 3x3 Matrices Matrix Multiplication Youtube
Why Is Matrix Multiplication Defined The Way It Is Quora

The Geometric Meaning Of Covariance In 2021 Geometric Inner Product Space Meant To Be

Part 22 Eigenvalues And Eigenvectors By Avnish Linear Algebra Medium