Matrix Chain Multiplication Complexity Analysis
Ie we want to compute the product A1A2An. We have many options to multiply a chain of matrices because matrix multiplication is associative.
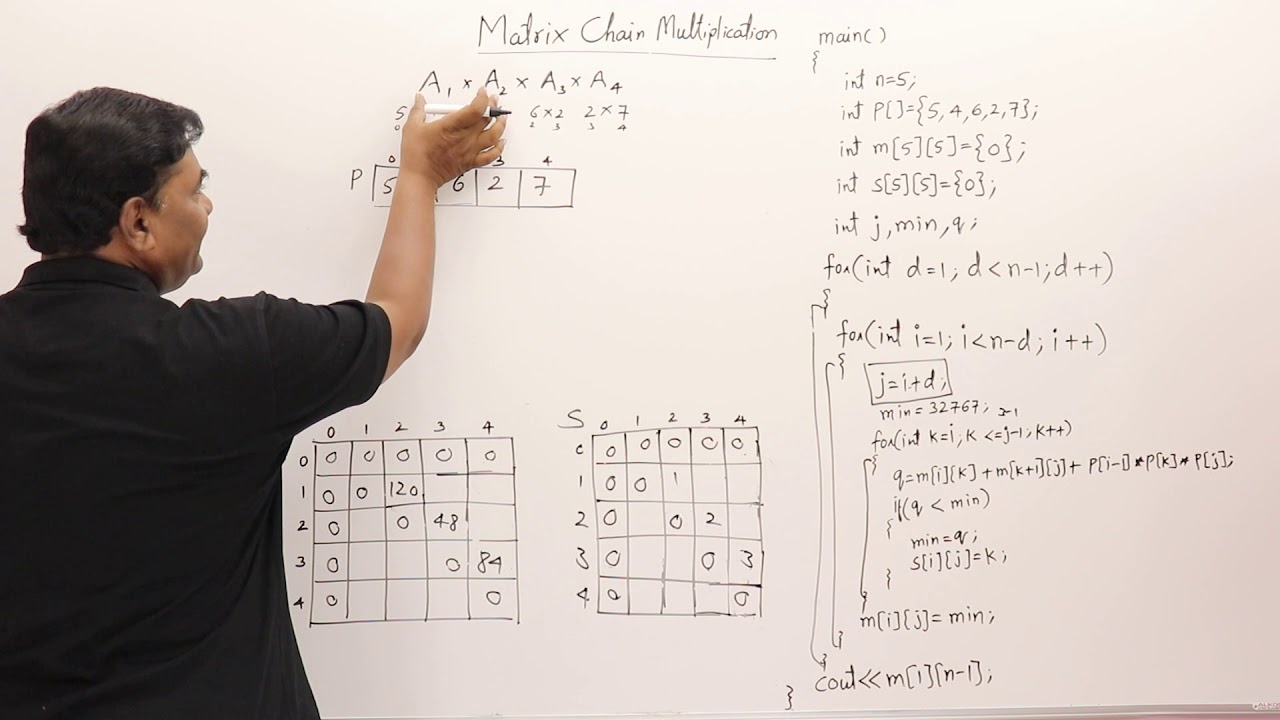
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube
M1 N-1will be the solution to the matrix chain multiplication problem.
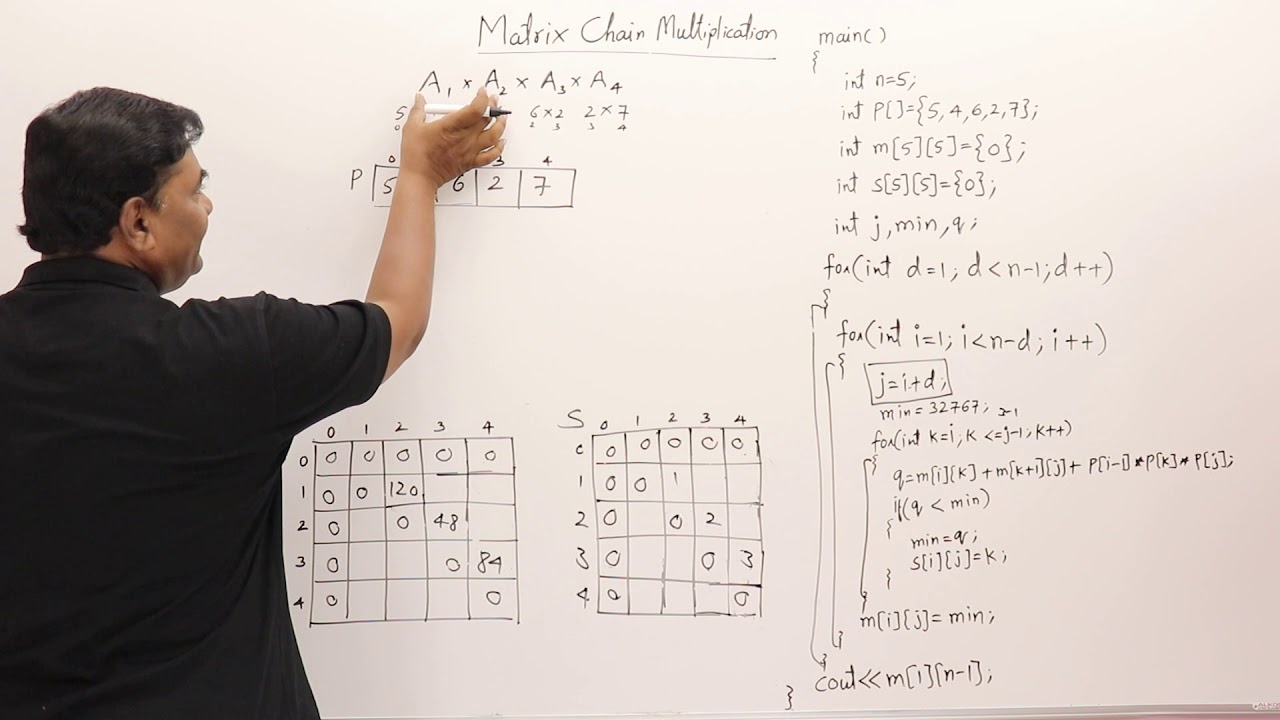
Matrix chain multiplication complexity analysis. In generalized way matrices A P x Q and B Q x. As Comparing both output 1140 is minimum in both cases so we insert 1140 in table and M 3 x M 4 M 5 this combination is chosen for the output making. We need to write a function MatrixChainOrder that should return the minimum number of multiplications needed to multiply the chain.
M 1 4 M 1 M 2 M 3 M 4. Mij 0 if ij min mik mk1. There are three cases by which we can solve this multiplication.
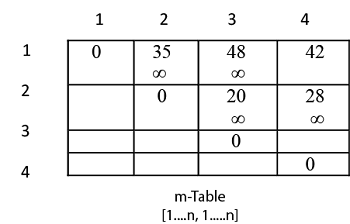
For example if we had four matrices A B C and D we would have. These estimates provide an insight into reasonable directions of search for efficient algorithms. P 40 20 30 10 30 Output.
Example of Matrix multiplication. Now Product of 4 matrices. To calculate each element we did 3 multiplications which is equal to number of columns in first matrix and number of rows in second matrix.
Length of array P number of elements in P length p 5 From step 3 Follow the steps in Algorithm in Sequence According to Step 1 of Algorithm Matrix-Chain-Order. ABCD AB CD A BCD. The loops are nested three deep.
Hence the time complexity is. Also space complexity is On2. Let A be a pq matrix and B be a qr matrix.
The objective is to parenthesize the matrix chain product A1A2A3An such that there are minimum number of scalar multiplications. So totally for 4 elements 43 12 multiplications are required. Algorithms asymptotic notation of running time complexity space and time complexity order of.
If cost mi j then update if better mi j cost. For AiAi1AkAk1Aj Matrix Ai has dimension pi-1xpi The author comes up with the recursion. We need to find the optimal way to parenthesize the chain of matrices.
Knapsack Matrix Chain Multiplication LCS Transitive Closure Floyd-Warshall 1. M 3 5 1140. Matrix chain multiplication is nothing but it is a sequence or chain A1 A2 An of n matrices to be multiplied.
N length p-1 Where n is the total number of elements And length p 5 n 5 - 1 4 n 4 Now we construct two tables m and s. Cost Mem-Matrix-Chainp i k Mem-Matrix-Chainp k 1 j pi 1 pk pj. Let the input 4 matrices be A B C and D.
Analysis of Algorithm is an important part of a broader computational complexity theory which provides theoretical estimates for the resources needed by any algorithm which solves a given computational problem. In other words no matter how we parenthesize the product the result will be the same. The Chain Matrix Multiplication Problem Given dimensions corresponding to matr 5 5 5 ix sequence 5 5 5 where has dimension determinethe multiplicationsequencethat minimizes.
26000 There are 4 matrices of dimensions 40x20 20x30 30x10 and 10x30. Each loop index takes on values. 43 out of 5 43 14 ratings 186 students.
Up to 15 cash back Data Structures Complexity AnalysisRecursion backtracking Dynamic ProgrammingGreedy algorithm Divide and Conquer Rating. Time complexity ofmatrix chain multiplication using dynamic programmingis On2. M 1 x M 2 x M 3 M 4.
Then the complexity is pqr.

Matrix Chain Multiplication Dynamic Programming Youtube
Matrix Chain Multiplication Algorithm Javatpoint

Matrix Chain Multiplication Ordering Procedure The Mcmo Complexity Is Download Scientific Diagram

Matrix Chain Multiplication Geeksforgeeks Youtube
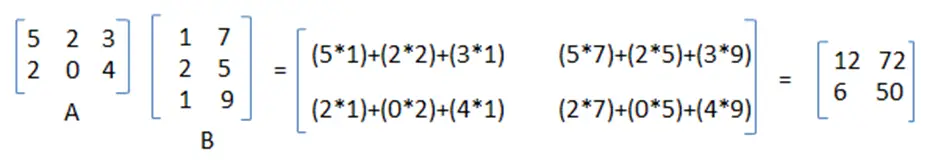
Matrix Chain Multiplication In C And C The Crazy Programmer

Unit 4 Dynamic Programming Ppt Video Online Download

4 3 Matrix Chain Multiplication Dynamic Programming Youtube

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube

Matrix Chain Multiplication Ppt Download






