Matrices Do Not Have Multiplicative Inverses
Other answers state basically that for a matrix to be invertible their multiplication should be commutative by definition. Having a multiplicative inverse Having full rank Having a nonzero determinant Representing a linear transformatio.

What Is An Inverse Matrix Mathbootcamps
The area of a triangle with vertices x 1 y.

Matrices do not have multiplicative inverses. Multiplicative Inverses of Matrices and Matrix Equations. Because when you multiply them together you get the multiplicative identity one. In other words for the majority of matrices A there exists a matrix A-1 such that AA-1 I and A-1A I.
In order to find the multiplicative inverse we have to find the matrix for which when. Suppose A is equal to a nonzero matrix of second order. Regular matrices are characterized by any one of the following properties.
In arithmetic there is one number which does not have a multiplicative inverse. When A is multiplied by A -1 the result is the identity matrix I. Multiplicative inverses exist for some matrices.
AA -1 A -1 A I. This means if you row reduce to try to compute the inverse one of the rows will have only zeros which means there is no inverse. That equals 0 and 10 is undefined.
The other examples are similar with M having two rows or two columns one being a scalar multiple of the other. Non-square matrices do not have inverses. A square matrix is either regular or singular.
This can only be possible with square matrices. The additive inverse of the null vector is the null vector compare this to your definition. A A 1 A 1 A and should be equal to identity matrix.
The multiplicative inverse of a matrix A is written A -1. Inverses for Matrices that do NOT have Inverses Teaching Students How to Think like Mathematicians Professor Je Stuart Mathematics Department Pacic Lutheran University Tacoma WA 98447 USA jereystuartpluedu Pacic Lutheran University January 2010 Je Stuart Pacic Lutheran University Generalizing Inverses January 2010 1 14. There are matrices that have no multiplicative inverse but all matrices have an additive inverse.
This matrix has no inverse because the columns are not linearly independent. This section will deal with how to find the Identity of a matrix and how to find the inverse of a square matrix. Not all matrices have inverse matrices.
Matrices of this nature are the only ones that have an identity. Only a square matrix may have a multiplicative inverse as the reversibility displaystyle A A -1 A -1AI AA. The inverse matrix A1can be designated as.
But also the determinant cannot be zero or we end up dividing by zero. So matrices are powerful things but they do need to be set up correctly. First of all to have an inverse the matrix must be square same number of rows and columns.
A I A matrix that has a multiplicative inverse is called an invertible matrix. But this proof could be augmented with geometric intuition I guess. MULTIPLICATIVE INVERSES For every nonzero real number a there is a multiplicative inverse la such that Recall that la can also be written a -1.
Most matrices also have a multiplicative inverse. A vector has an additive inverse. A square matrix which has an inverse is called invertible or nonsingular and a square matrix without an inverse is called noninvertible or singular.
Not all square matrices have inverses. If A is a 2 x 2 matrix and A -1 is its inverse then AA -1 I 2. We cannot go any.
The same is true of matrices. In the rest of this section a method is developed for finding a multiplicative inverse for square matrices. The product of a matrix and its multiplicative inverse matrix is the multiplicative identity matrix.
The term inverse is always related to a binary operation. A square matrix is one in which the number of rows and columns of the matrix are equal in number. Consider M 11 11.
The multiplicative inverse of a real number is the number that yields 1 the identity when multiplied by the original number. The Inverse May Not Exist. ESSENTIAL UNDERSTANDING 4-3 Determinants and Inverses 130 Lesson 4-3 Determinants and Inverses.
Is the multiplicative inverse of a because a 1. The product of a matrix A and its inverse A1must equal the identity matrix I for multiplication. The modular inverse of a number refers to the modular multiplicative inverseFor any integer a such that a p 1 there exists another integer b such that ab 1 mod pThe integer b is called the multiplicative inverse of a which is denoted as b a 1Modular inversion is a well-defined operation for any finite ring or.
Anything you multiply say M C will not give I because both rows of MC will be the same. Tom St Denis Greg Rose in BigNum Math 2006. Unfortunately not all matrices will have an inverse nor is finding the multiplicative inverse that simple.
There are other square matrices without inverses.
Multiplicative Inverses Of Matrices And Matrix Equations Video Lesson Transcript Study Com

Question Video Finding The Inverse Of A Diagonal Matrix Nagwa

Inverse Matrix Matrix Multiplication Youtube

2 5 Determinants And Multiplicative Inverses Of Matrices Objectives 1 Evaluate Determinants 2 Find The Inverses Of Matrices 3 Solve Systems Of Equations Ppt Download

Question Video Checking Whether A Matrix Is Invertible Nagwa

Multiplicative Inverses Of Matrices And Matrix Equations Video Lesson Transcript Study Com

Matrix Inverse Multiplicative Youtube

2 5 Determinants And Multiplicative Inverses Of Matrices Objectives 1 Evaluate Determinants 2 Find The Inverses Of Matrices 3 Solve Systems Of Equations Ppt Download

Are Two Matrices Inverses Of Each Other Youtube

What Is An Inverse Matrix Mathbootcamps

Find The Multiplicative Inverse Of A Matrix Youtube

Question Video Finding The Inverse Of A Matrix Nagwa
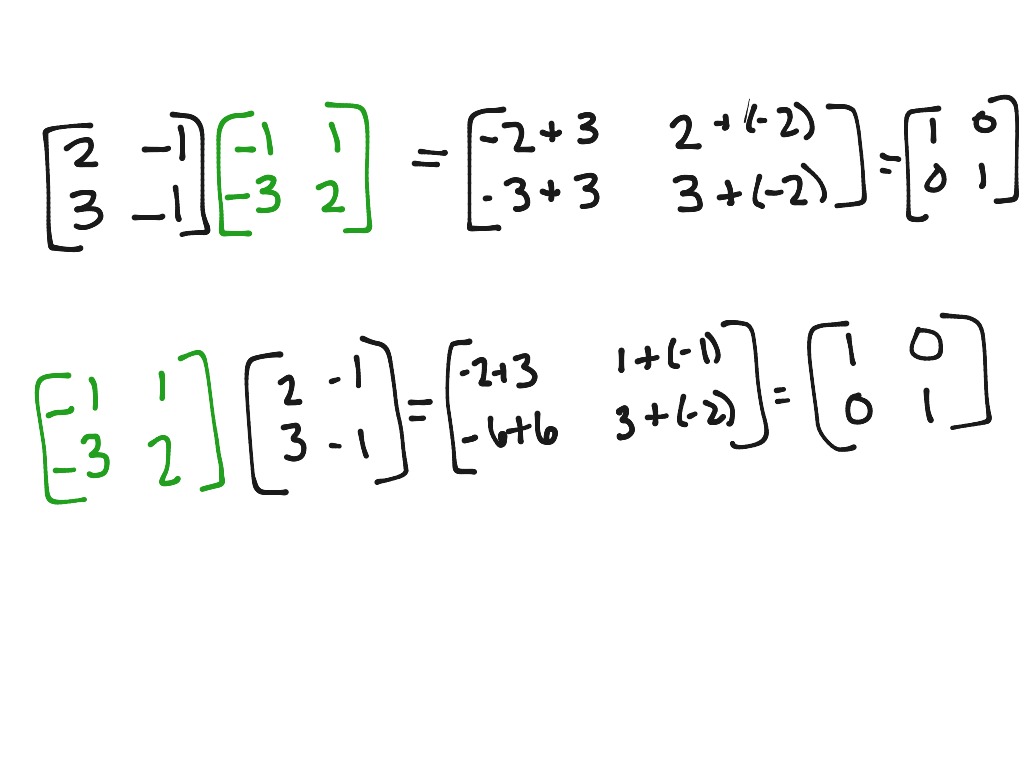
Multiplicative Inverse Matrix Math Algebra Showme

Multiplicative Inverse An Overview Sciencedirect Topics

2 5 Determinants And Multiplicative Inverses Of Matrices Objectives 1 Evaluate Determinants 2 Find The Inverses Of Matrices 3 Solve Systems Of Equations Ppt Download

Multiplicative Inverses Of Matrices And Matrix Equations Video Lesson Transcript Study Com

Zero Identity And Inverse Matrices Solutions Examples Videos Worksheets Games Activities

