Symmetric Matrix Dot Product

24 Jul, 2021

X y Dot x B. It is a dot product of rows and of the original matrix.

1 7 Diagonal Triangular And Symmetric Matrices Ppt Download

Inverse of a symmetric matrix is symmetric if it exists.

Symmetric matrix dot product. Any help is greatly appreciated thank-you in advance. Where superscript T refers to the transpose operation and a is defined by. Mv Ma 1v 1 a nv n 2 6 6 6 4 a 1 a 2.

Is an inner product on V if and only if. The matrix 1 1 0 2 has real eigenvalues 1 and 2 but it is not symmetric. The dot product of two matrices multiplies each row of the first by each column of the second.

If no give a counter-example. Mx AMy where Ais a self-adjoint matrix with positive eigenvalues 5 where M. And if and we have both and are inverses of but inverse is unique so B is symmetric.

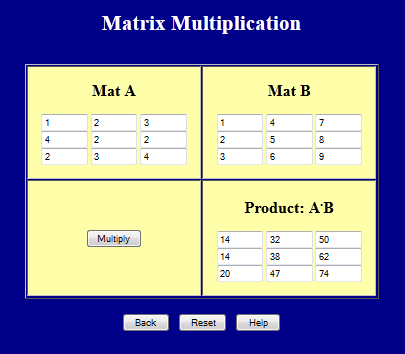
If Ais symmetric then A AT. 18 If A aijis an m n matrix and B bijis an n p matrix then the product of A and B is the m p matrix C cijsuch that. SYMMETRIC MATRICES AND INNER PRODUCTS 3 True or False Provide reasons for the true and counterexamples for the false.

For complex vectors the first vector is conjugated. Thus the linearity in the first argument is satisfied. Cij AikBkj C i j A i k B k j.

A matrix Ais symmetric is A AT. So langle Ah xranglexT Ah and langle h AT xrangleATxThxTAhlangle Ahxrangle Also ATA as A is symmetric and this gives the last equality. MatrixForm B A - Transpose A 0 4 3 0 4 0 2 1 3 2 0 5 0 1 5 0 1 B Transpose B True.

TrZ is the trace of a real square matrix Z ie TrZ P i Z ii. X y z x y T A z x T y T A z x T A z y T A z x z y z. If A is symmetric then Ax y xTATy xTAy xAy.

Let Abe a symmetric n nmatrix. Note that inner product can be written as. If V P 2R then the following is an inner product on V.

A 2 4 1 2 2 2 1 2 2 2 1 3 5 iiGive an example of a symmetric 3 3-matrix. Every real n -by- n matrix B is skew symmetric if and only if Dot B. A n 3 7 7 7 5 Example.

Multiplication rules are in fact best explained through tensor notation. Next for any vectors x y z and any real number r we have. If yes explain why.

Symmetric matrices and dot products Proposition An n n matrix A is symmetric i for all xy in Rn Ax y xAy. A dot-product on a vector space H is a symmetric bilinear form. I have the following question.

Compute the dot product between two vectors. Then xy 0. R x y r x T A y r x T A y r x y.

X n 3 5 Notice that quadratic forms are not linear transformations. The transpose matrix and dot products Problem 1. We can alternatively de ne a matrix Q to be symmetric if QT Q.

A 0b 02a 0b 13a 0b 22a 1b 02a 1b 14a 1b. Let A i j be a symmetric tensor and let B i j be an antisymmetric tensor. Dot also works on arbitrary iterable objects including arrays of any dimension as long as dot is defined on the elements.

Prove that the inner product of A i j and B i j is zero How would I go about doing this. Dotx y x y. Iii If Aand Bare symmetric n n-matrices is ABnecessarily symmetric.

H x H ℜ xx suchth th that i 0 xH ii 0 if and only if x 0ii 0 if and only if x 0 note that for thenote that for the canonical bilinear formcanonical bilinear form in ℜd xTAx. IIs the following matrix symmetric. 2 A symmetric matrix is always square.

Dot is semantically equivalent to sumdotvxvy for vxvy in zipx y with the added restriction that the arguments must have equal lengths. The vector cross product also can be expressed as the product of a skew-symmetric matrix and a vector. Fn is the usual coordinate map given by.

Here Rm nis the space of real m nmatrices. Dot Product and Matrix Multiplication DEFp. We denote the identity matrix ie a matrix with all 1s on the diagonal and 0s everywhere else by I that is I 1 0.

17 The dot product of n-vectors. Conversion to matrix multiplication. The matrix inner product is the same as our original inner product.

If Ais an m nmatrix then its transpose is an n m. The quadratic form associated to Ais the function Q A. Thus the function is symmetric.

In the special case where the matrix Ais a symmetric matrix we can also regard Aas de ning a quadratic form. Dot product is symmetric so the same is on the coordinate. Corollary If A is symmetric and xy are eigvecs corresponding todi erent eigvals.

For every square matrix A the matrix A - Transpose A is skew symmetric. Q Ax xAx is the dot product xTAx x 1 x n A 2 4 x 1. If equality holds for all xy in Rn let xy vary over the standard basis of Rn.

A symmetric matrix is a square matrix Q ℜnn with the property that Qij Qji for all ij 1n. I know that A i j A j i and B i j B j i but Im not too sure how this helps. The columns a i of the skew-symmetric matrix for a vector a can be also obtained by calculating the cross-product with unit vectors ie.

Products are often written with a dot in matrix notation as A B A B but sometimes written without the dot as AB A B. 1 Any real matrix with real eigenvalues is symmetric. And note that I is a symmetric matrix.

U a1anand v b1bnis u 6 v a1b1 anbn regardless of whether the vectors are written as rows or columns. The standard inner product between matrices is hXYi TrXTY X i X j X ijY ij where XY 2Rm n.

1 7 Diagonal Triangular And Symmetric Matrices Diagonal