How Do You Know If A Matrix Is Linearly Dependent
Have a look at the videos of rank. The following statements are equivalent.
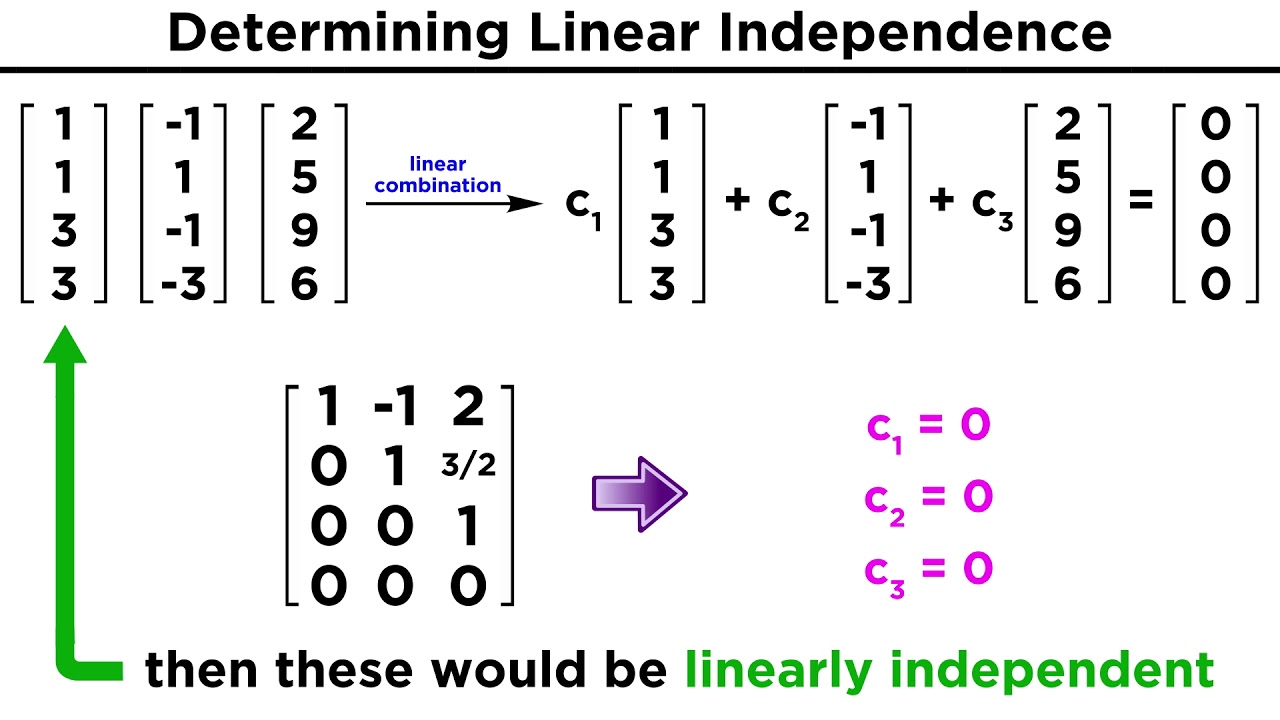
3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 Determine if the columns of A are linearly independent or dependent.

How do you know if a matrix is linearly dependent. C n y n x. Example The vectors u v and w are dependent since the determinant is zero. Vectors a b c are linearly dependent.
If r 2 and at least one of the vectors in A can be written as a linear combination of the others then A is said to be linearly dependent. You can use elementary row operations to zero out the leading elements in subsequent rows making the matrix upper triangular. When the determinant of a matrix is zero its rows are linearly dependent vectors and its columns are linearly dependent vectors.
What is linear independence. Check whether the vectors a 1. Yes it is related.
α1 -2 α2 for example α2 1 α1 -2 and this means that the rows s1 and s2 are linearly dependent. Y x c 1 y 1 x c 2 y 2 x. 1 b 1.
On the other hand if no vector in A. Det0 IFF the rows are linearly dependent. In the theory of vector spaces a set of vectors is said to be linearly dependent if there is a nontrivial linear combination of the vectors that equals the zero vector.
α1 2 α2 0. How to find out of a set of vectors are linearly independent. If the determinant is non zero then the vectors are linearly independent.
Let A be an m n matrix and let T x Ax be the associated matrix transformation. For every b in R m the equation T x b has at most one solution. Row reduce your matrix and see which of the situations you have.
These concepts are central to the definition of dimension. Let A 0 3 9 2 1 7 1 4 5 1 4 2 First operation I perfomed was switch r1 to r4 and -2r1r2. 2 are linearly independent.
0 c 0. Divide the first equation by 2 and the second equation by 5. A 1 4 2 0 9 3 1 4 5 0 3 9 Next performed was r 1 r 3 to get.
Is a 23 matrix invertible. Otherwise they are linearly dependent. For linearly independent solutions represented by y 1 x y 2 x y n x the general solution for the n th order linear equation is.
For every b in R m the equation Ax b has a unique solution or is inconsistent. α1 2 α2 0. Matrices with linearly dependent rows will have the last row s be all 0s because they were linear combinations of the row s above.
By doing gaussian elimination you will see that at least one of the rows will only contain zeros if they are linearly dependent. The motivation for this description is simple. A set of n vectors of length n is said to be linearly dependent when the determinant of matrix with these vectors as columns is zero.
In the theory of vector spaces a set of vectors is said to be linearly dependent if one of the vectors in the set is a linear combination of the others. If no such linear combination exists then the vectors are said to be linearly independent. Calculate the coefficients in which a linear combination of these vectors is equal to the zero vector.
The solution of this system may be any number α1 and α2 such that. Let A 1 4 2 0 9 3 0 0 7. The set is of course dependent if the determinant is zero.
How can it be seen if the following matrix is linear dependent. If the determinant of a square matrix nn A is zero then A is not invertible. Example The vectors and are linearly independent since the matrix has a non-zero determinant.
You can take the vectors to form a matrix and check its determinant. If a system is linearly dependent at least one of the vectors can be represented by the other vectors. In this video well go through an example.
At least one of the vectors depends linearly on the others. Then you havs shown that one row of the matrix is a linear combination of the other rows and hence the rows are linearly dependent. Means vectors a b c are linearly dependent.

What Is The Difference Between Linearly Independent And Linearly Dependent Quora

How To Find Out If A Set Of Vectors Are Linearly Independent An Example Youtube

Linear Algebra Example Problems Linearly Independent Vectors 1 Youtube

The Determinant Essence Of Linear Algebra Chapter 6 Youtube Algebra Online Math Classes Online Math
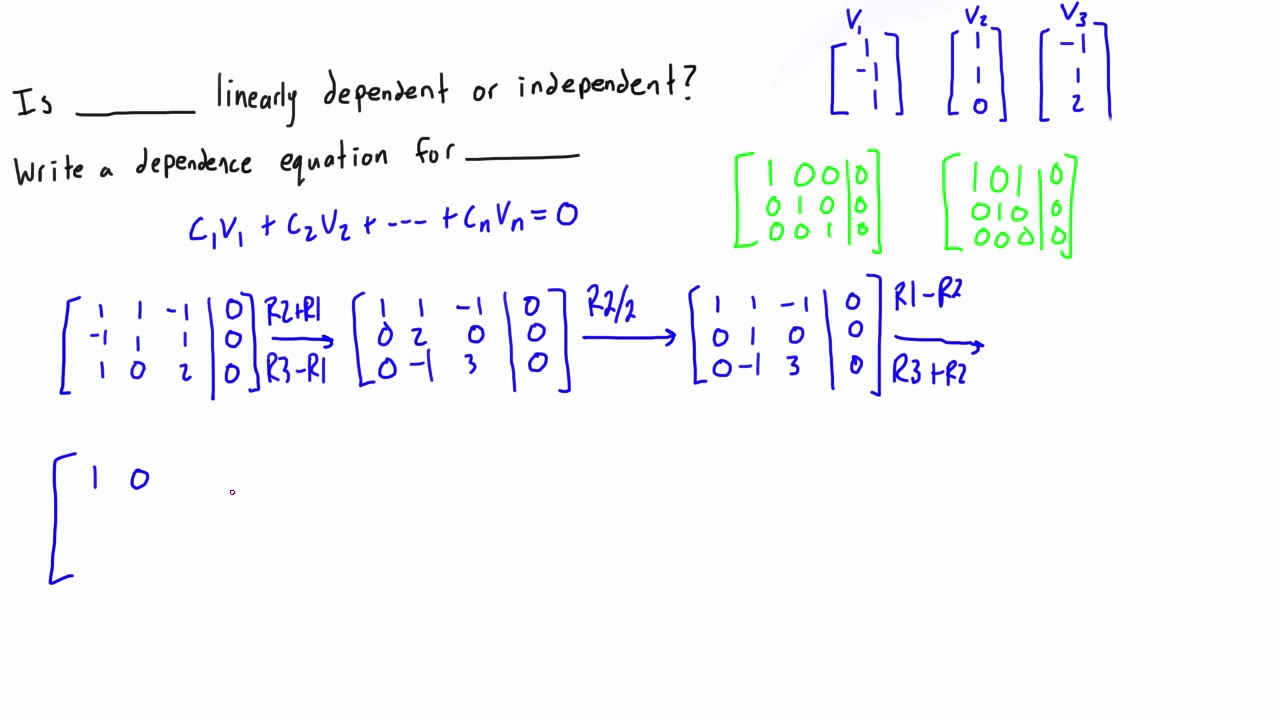
How To Determine If A Set Of Vectors Are Linearly Dependent Or Independent Youtube

Linear Algebra Example Problems Linearly Independent Vectors 1 Youtube

Determining If Functions Are Linearly Independent Or Dependent Using The Definition Math Videos Differential Equations Algebra