Symmetric Matrices Nonsingular
A sufficient condition for a symmetric n n matrix C to be invertible is that the matrix is positive definite ie. AbstractLet Q_n denote a random symmetric n by n matrix whose upper diagonalentries are iid.
Symmetric Matrices Linear Algebra
If a matrix has some special property eg.

Symmetric matrices nonsingular. In the latter case A is also nonsingular. If A does not have an inverse A is called singular. Let A aid be a sign-nonsingular skew-symmetric matrix of order m let 1 _ r s m such that a.
If A is a skew-symmetric matrix which is also a square matrix then the determinant of A should satisfy the below condition. An n n matrix A is called nonsingular or invertible if there exists an n n matrix B such that AB BA I. The proof uses a quadraticversion of Littlewood-Offord type results concerning the concentrationfunctions of random variables and can be extended for more general models ofrandom matrices.
4 0 and let B be the matrix obtained from A by replacing arrs and ar with zeros. A is positive definite if and only if all of its eigenvalues are 0. Let S Be A Skew-symmetric Matrix With Real Entries.
For Matrices Such That The Product AB Is Defined Explain Why. I Let A be a symmetric nonsingular matrix. Thus the zero vector Oin S and the condition 1 is met.
It follows that is positive definite if and only if both and are positive definite. Consider The Block Matrix M Rex Bxs Suppose That Both A And SB-RA-C Are Nonsingular. We prove that Q_n is non-singular with probability1-On-18delta for any fixed delta 0.
1 point Determine whether the given set S is a subspace of the vector space V. To show that AB in S we need to check that the matrix AB is symmetric. Symmetric block matrices.
Positive definite matrices are even bet ter. Often appear in applications. To prove that the inverse of A is symmetric you need to show that A 1 T A 1.
Otherwise is called singular. Prove that the inverse of a symmetric nonsingular matrix is symmetric. V MnR and S is the subset of all symmetric matrices B.
Show that if B is an arbitrary m times n matrix then the m times m matrix given by the product B A BmathrmT is symmetric. A canonical form of with respect to congruence transformations was given by Sergeichuk 1988 up to classification of symmetric and Hermitian forms over finite extensions of. Symmetric matrices A symmetric matrix is one for which A AT.
Thus we have the following. Which shows that is congruent to a block diagonal matrix which is positive definite when its diagonal blocks are. The zero vector O in V is the n times n zero matrix and it is symmetric.
C Show that an matrix is nonsingular if and only if. Let be a field of characteristic not and let be a pair of matrices over in which is symmetric and is skew-symmetric. In this video we prove that if A is a nonsingular skew symmetric matrix then A 1 is skew symmetric.
Symmetric matrices are good their eigenvalues are real and each has a com plete set of orthonormal eigenvectors. A symmetric matrix A is positive semidefinite if and only if all of its eigenvalues are 0. For the best math tutoring and math vid.
The determinant of skew symmetric matrix is non-negative. X R n 0 x T C x 0. The following is a ready consequence.
Prove That I -S Is Nonsingular. B Show that if is nonsingular then the column vectors of are linearly independent. If A I S1-5-1 Show That A-1 AT.
If is nonsingular then we can write. We can use this observation to prove that A T A is invertible because from the fact that the n columns of A are linear independent we can prove that A T A is not only symmetric but also positive definite. Determinant of Skew Symmetric Matrix.
So a non symmetric matrix is one which when transposed gives a different matrix than the one you started with. V R and S is the set of solutions to the homogeneous linear. Sign-nonsingular skew-symmetric matrices are investigated.
The concept of a nonsingular graph is introduced and such graphs are related to pfaffian graphs. Bernoulli random variables which take values 0 and 1 withprobability 12. We obtain a simpler canonical form of if is nonsingular.
Its a Markov matrix its eigenvalues and eigenvectors are likely. Ii This means that A T A and A 1 exists. Show that if A is a nonsingular symmetric n times n matrix then A-1 is symmetric.
A symmetric matrix is a matrix which does not change when transposed. When identity matrix is added to skew symmetric matrix then the resultant matrix is invertible. V is the vector space of all real-valued functions defined on the interval -0 0 and S is the subset of V consisting of those functions satisfying f0 0.
All of the eigenvalues of a variance-covariance matrix. To check the second condition take any A B in S that is A B are symmetric matrices. A Show that if and are nonsingular matrices then the product is also nonsingular.
It is easy to see that B is a sign-nonsingular skew-symmetric matrix if and only if B is a nonsingular matrix. Det A T det -A -1 n detA. An matrix is called nonsingular if the only solution of the equation is the zero vector.
The identity matrix is symmetric whereas if you add just one more 1 to any one of its non diagonal elements then it becomes non symmetric. Prove That ---------.

Symmetric Matrix An Overview Sciencedirect Topics

13 Adjoint Of Matrix Mathematics Prof Matrix

Let A Be A Nonsingular Matrix With Inverse A 1 1 2 Chegg Com
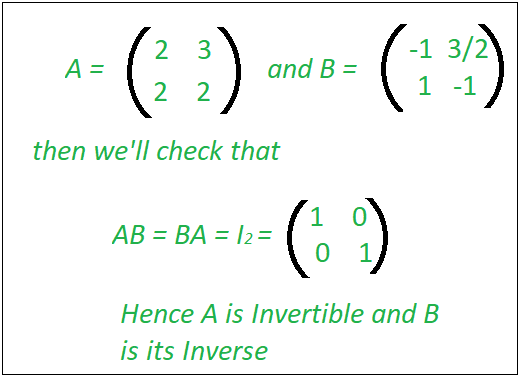
Check If A Matrix Is Invertible Geeksforgeeks

Symmetric Matrix Don T Memorise Youtube

15 Inverse Of A Square Matrix Dear Students Mathematics Lecture

2 Algebra Of Matrices Addition Subtraction Of Matrices Multiplicat Matrix Multiplication Subtraction Algebra

2 A I Give The Definition Of N N Symmetric Matrix Chegg Com

Singular Matrix And Non Singular Matrix Don T Memorise Youtube

Sec 2 3 Symmetric Matrices Youtube

Http Www Aplustopper Com Find Lines Symmetry Symmetry How Do You Find Lines

The Inverse Of An Invertible Symmetric Matrix Is A Symmetric Matrix Youtube

17 Rank Of Matrix By Determinant Method Dear Students Matrix Mathematics

Question1 A I Suppose A And B Are Nonsingular Chegg Com

Matrices And Determinants Part 1 G Mathematics Basic Maths F Sc P Basic Math Mathematics Matrix
Q 16 If A Is Non Singular Then Show That A 1 A Chegg Com




