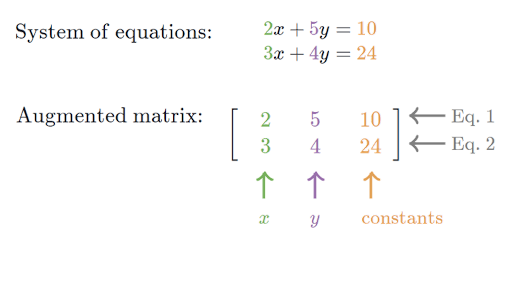Multiplying A Row Of An Augmented Matrix Through By Zero

The second column of B was -1 3. Use row operations to obtain zeros down the first column below the first entry of 1.

Determining The Concavity Of A Function 12th Maths Math Function

The first equation should have a leading coefficient of 1.

Multiplying a row of an augmented matrix through by zero. Multiplying a row of an augmented matrix through by a zero is an acceptable elementary row operation. Swap the positions of two rows. If x2 is 1 we get 0 1 5 0 is an answer.

Multiplying a linear equation through by zero is an acceptable elementary row operation. D A single linear equation with two or more unknowns must have infinitely many solutions. Let A 3 6 2 4 Construct a 2 2 matrix B such that A B is the zero matrix.

C The linear system x y 3 2x 2y k cannot have a unique solution regardless of the value of k. If the matrix is associated to a system of linear equations then these operations do not change the solution set. Therefore the 5 came from adding up the products of multiplying each element of row 1 of the left matrix A with each element of column 2 of the right matrix B.

A A linear system whose equations are all homogeneous must be consistent. This corresponds to adding the second row of the matrix to the third row of the matrix which is notated by R 3 R 3 R 2. Use row operations to obtain zeros down the first column below the first entry of 1.

B Multiplying a rov of an augmented matrix through by zero is an acceptahlc elementary row operation. B Multiplying a row of an augmented matrix through by zero is an acceptable elementary row operation. The linear system x - y 3.

Because we can have any value for x2 that means any multiple of that line PASSING THROUGH 2 0 5 0 is an answer. A A linear system whose equations are all homogeneous must be consistent b Multiplying a row of an augmented matrix through by zero is an acceptable elementary row operation. C The linear system 5 y3 2x 2y k cannot have a unique solution regardless ofthe value k.

Use row operations to obtain a 1 in row 2 column 2. Given an augmented matrix perform row operations to achieve row-echelon form. The value of A B would be.

Which has the augmented matrix To solve this system of equations a standard method is to transform the system into an equivalent system with an augmented matrix of the form and corresponding equations ax by cz d 1 ey fz g 2 hz i 3 where a 0 and e 0 and h 0 The above system can be solved using back-substitution. This process is pictured for all 4 positions of the answer in. There are three types of elementary row operations which may be performed on the rows of a matrix.

D A single linear equation with two or more unknowns must have infinitely many solutions. Interchange rows or multiply by a constant if necessary. 3 b 11 6 b 12 0 2 b 11 4 b 12 0.

Multiply row with a non-zero constant row multiplication 3 Add a row to another row row addition 4 Add a row that has been multiplied with a nonzero constant to another row Row multiplication and row addition can be combined together Example 2. Use two different nonzero columns for B. 1 1 2 0 0 0 1 2 2 4 0 1 2 1 2 We continue by adding the second equation to the third equation.

X 1 1 2 x 2 0 1 2 x 2 2 x 3 4 1 2 x 2 x 3 2. 1 0 h 0 1 k 1 0 h 0 1 k Once we have the augmented matrix in this form we are done. The first row of A was 1 2.

This makes a line that goes through 2 0 5 0. Add to one row a scalar multiple of another. We multiply 1-1 and 23 to get -1 and 6 which we add to get 5 the element in row 1 column 2 of the answer.

A B 3 b 11 6 b 12 3 b 21 6 b 22 2 b 11 4 b 12 2 b 21 4 b 22 I was thinking of using substitution but the following equations just result in the variables equalling 0. C The linear system x - y 3 2x - 2y k cannot have a unique solution regardless of the value of k. B Multiplying a row of an augmented matrix through by zero is an acceptable elementary row operation The linear system - y 3 2x - 2y k cannot have a unique solution regardless of the value of k.

The ith row vector of a matrix product AB can be computed by multiplying A by the ith row vector of B. Multiply a row by a non-zero scalar. The first equation should have a leading coefficient of 1.

So if x2 is 0 we get 2 0 5 0 as an answer. Interchange rows or multiply by a constant if necessary. Given an augmented matrix perform row operations to achieve row-echelon form.

Axby p cxdy q a x b y p c x d y q. We first write down the augmented matrix for this system a b p c d q a b p c d q and use elementary row operations to convert it into the following augmented matrix. Row Echelon Form A matrix is said to be in.

Augmented Matrices Reduced Row Echelon Form Youtube

6 1 Matrices And Systems Of Equations

Augmented Matrix An Overview Sciencedirect Topics

Examples Of Systems Of Equations

Reduced Row Echelon Form Rref Caclulator Emathhelp Form The Row Reduced

Pin On Cheat Sheets

Representing Linear Systems With Matrices Article Khan Academy

Solved Find A Matrix P12 So That Multiplying By P12 On Th Chegg Com

Augmented Matrices Row Echelon Form Youtube

Augmented Matrices With 0 1 Or Infinite Solutions 141 44 Youtube

Augmented Matrices Reduced Row Echelon Form Youtube

Pin On Shaders Math

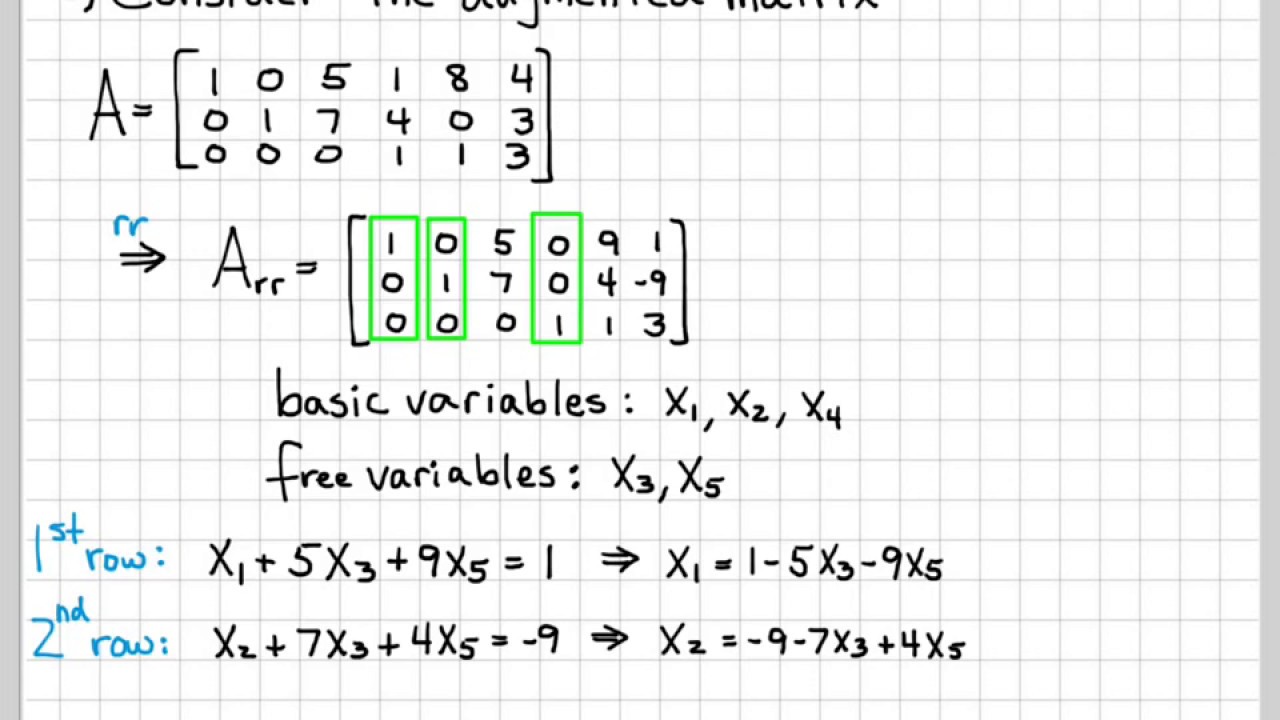
Linear Algebra Example Problems General Solution Of Augmented Matrix Youtube

Hi Everyone I M Officially A Week Into My Sophomore Year Of University Yes My University Year Starts In Study Notes Notes Inspiration Bullet Journal Writing

Pin On School

How To Perform Matrix Row Operations Video Lesson Transcript Study Com

Examples Of Systems Of Equations

Chapter 1 Systems Of Linear Equations And Matrices

Section 8 2 Operations With Matrices Math Notes And