Matrix Chain Multiplication Code In Python
Problem Description In the matrix-chain multiplication problem we are given a sequence of matrices A1 A2 An. We can treat each element as a row of the matrix.

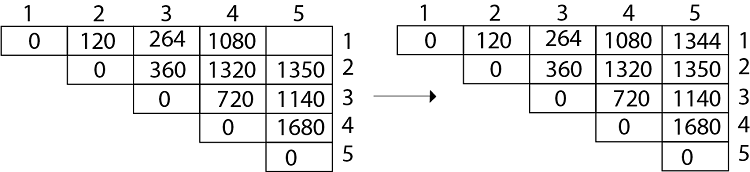
Matrix Chain Multiplication Explained Kilichbek Haydarov
Then ABC 10305 10560 1500 3000 4500 operations A BC 30560 103060 9000 18000 27000 operations.
Matrix chain multiplication code in python. We need to write a function MatrixChainOrder that should return the minimum number of multiplications needed to multiply the chain. M ii 0 compute smallest matrix costs first for chains of length 2 to n. Let the input 4 matrices be A B C and D.
J i l-1 j is the endpoint of the chain. The first row can be selected as X 0. N len p -1.
Given an array p which represents the chain of matrices such that the ith matrix Ai is of dimension p i-1 x p i. So just to clarify how matrix multiplication works you multiply the rows with their respective columns. This can be done using the following code.
Def matrix_chain_multiply pij. The minimum number of multiplications are obtained by putting parenthesis in following way ABCD -- 102030 103040 104030 Input. The problem is not actually to perform the multiplications but merely to decide the sequence of the.
P 40 20 30 10 30 Output. Let the input 4 matrices be A B C and D. The basic algorithm is as follows.
Clearly the first parenthesization requires less number of operations. Let the input 4 matrices be A B C and D. M ij Minimum number of scalar multiplications ie cost needed to compute the matrix A iA.
A is a 10 x 30 matrix B is a 30 x 5 matrix and C is a 5 x 60. P 10 20 30 Output. M 0 for x in xrange 0 n for y in xrange 0 n s 0 for x in xrange 0 n for y in xrange 0 n for i in xrange 0 n.
The first Value of the matrix must be as follows. In this particular problem we will determine how to arrange the matrices in order to perform the multiplication with least cost. Multiplication of two matrices X and Y is defined only if the number of columns in X is equal to the number of rows Y.
Given an array p which represents the chain of matrices such that the ith matrix Ai is of dimension p i-1 x p i. We need to write a function MatrixChainOrder that should return the minimum number of multiplications needed to multiply the chain. 34 rows For example.
N dimslength - 1. In Python we can implement a matrix as nested list list inside a list. Given a sequence of matrices the goal is to find the most efficient way to multiply these matrices.
For k in range ij. MatrixChainMultiplication int dims. For i in 0.
Cij min Cik Ck1j di-1dkdj where i. Use the pseudo-code in the book 152 in order to implementmatrix chain multiplication in Python or C. Let the input 4 matrices be A B C and D.
The program shouldprint out the costs of the best implementation as well as the bestparenthesizationDeliverables in printYour code nicely formatted now pasting into MS Word withoutediting the style The output for the following cases where thesequence of dimensions isa. For i in xrange 0 n-l 1. Let j i lg optmij Naturalhigh for k in i.
P 40 20 30 10 30 Output. This is a Python program to solve matrix-chain multiplication using dynamic programming with top-down approach or memoization. For example X 1 2 4 5 3 6 would represent a 3x2 matrix.
Clearly the first parenthesization requires less number of operations. 11 24 3 7 1 8 21 30. Def matrix_chain_order p.
26000 There are 4 matrices of dimensions 40x20 20x30 30x10 and 10x30. 26000 There are 4 matrices of dimensions 40x20 20x30 30x10 and 10x30. 26000 There are 4 matrices of dimensions 40x20 20x30 30x10 and 10x30.
Find the best order for matrix chain multiplication. Matrix chain multiplication or Matrix Chain Ordering Problem MCOP is an optimization problem that can be solved using dynamic programming. Length dims n 1.
Countmatrix_chain_multiply pikmatrix_chain_multiply pk1jp i-1p kp j if count. Let n optdimshigh optm newSeqWithn newSeqNaturaln opts newSeqWithn newSeqNaturaln for lg in 1. Then ABC 10305 10560 1500 3000 4500 operations A BC 30560 103060 9000 18000 27000 operations.
For l in xrange 2 n 1. And the element in first row first column can be selected as X 0 0. Let cost optmik.
P 40 20 30 10 30 Output. 6000 There are only two matrices of dimensions 10x20 and 20x30. Now see our Python code below.
It is time to loop across these values and start computing them. We need to write a function MatrixChainOrder that should return the minimum number of multiplications needed to multiply the chain. Length lenp lenp number of matrices 1 mij is the minimum number of.

Template Metaprogramming 41 Matrix Chain Multiplication In C Dynamic Programming 1 2 Youtube

4 3 Matrix Chain Multiplication Dynamic Programming Youtube
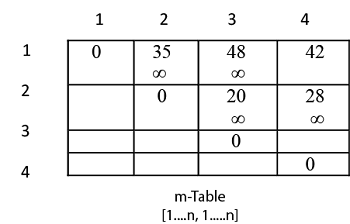
Matrix Chain Multiplication Algorithm Javatpoint

Matrix Chain Multiplication In C Codespeedy
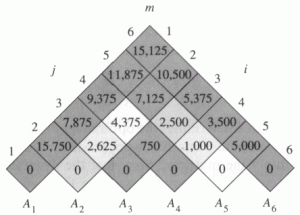
How To Solve Matrix Chain Multiplication Using Dynamic Programming Algorithms Blockchain And Cloud

Optimum Order For Matrix Chain Multiplications Prismoskills

Matrix Chain Multiplication Geeksforgeeks Youtube
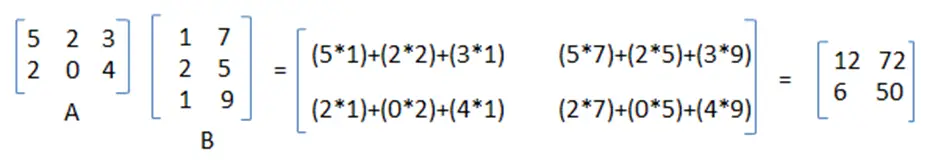
Matrix Chain Multiplication In C And C The Crazy Programmer

Matrix Chain Multiplication Explained Kilichbek Haydarov
Madamwar Matrix Chain Multiplication Dynamic Programming
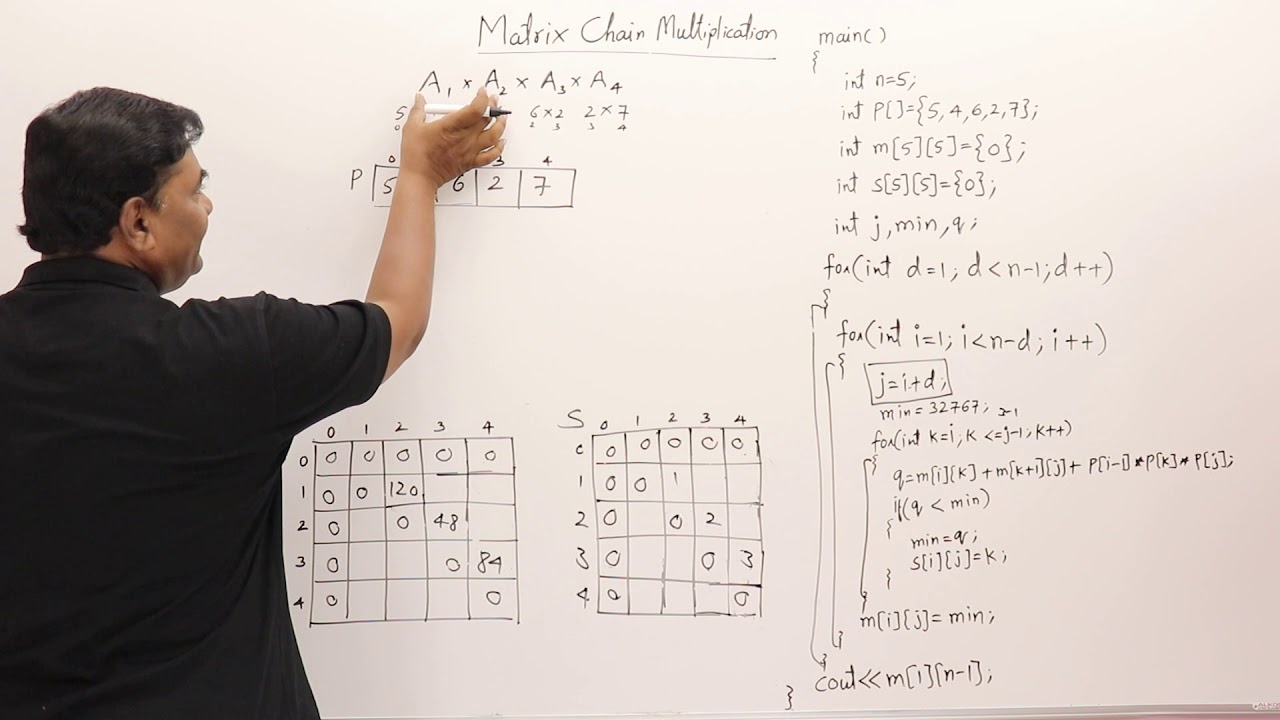
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube

Matrix Chain Multiplication Explained Kilichbek Haydarov
Matrix Chain Multiplication Using Dynamic Programming Algotree

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube

Matrix Chain Multiplication Using Dynamic Programming A Visual Tutorial Visutorial Youtube

Matrix Chain Multiplication Dp 8 Tutorialspoint Dev

Use The Pseudo Code In The Book 15 2 In Order Chegg Com

Matrix Chain Multiplication Matrix Chain Multiplication Is An By Vaibhavi Maradiya Medium