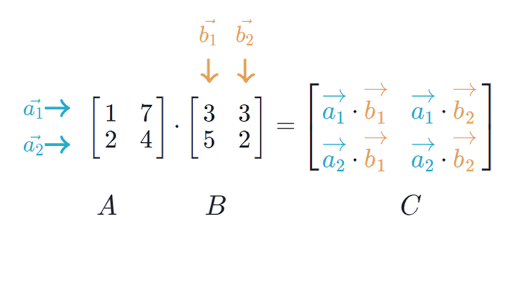Explain In Detail The Chain Matrix Multiplication With Relevant Procedure

05 Jun, 2021

The the transition matrix. The number of operations are - 203010 402010 401030 26000.

Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks

One of the very popular programs in C programming is Matrix Multiplication.

Explain in detail the chain matrix multiplication with relevant procedure. Basic case else mi j infinity. Which is the matrix multiplication of and. We then use these results to compute Cs submatricies.

To begin constructing the supply chain strategy for your enterprise build a matrix. 1 Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram. Each matrix has fixed number of rows and columns and for multiplication to be feasible the number of rows of first matrix must be equal to number of columns of second matrix.

Say the matrices are named as A B C D. Initialize for k i to j 1 do try all possible splits costRec-Matrix-Chainp i. Markov chain each state jwill be visited over and over again an in nite number of times regardless of the initial state X 0 i.

N 4 arr 10 30 5 60 Output. Matrix A a b matrix B e f c d g h There will be 8 recursive calls. Practitioners and educators need a common definition of supply chain management and a shared understanding of the processes.

On the y axis identify your selection of say four attributes from the above list that best describes the Availability objectives of your organisation. In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions. If i j return 0.

This strategy is called Divide and Conquer. For example if the rat in the closed maze starts o in cell 3 it will still return over and over again to cell 1. In this eight multiplication and four additions subtraction are performed.

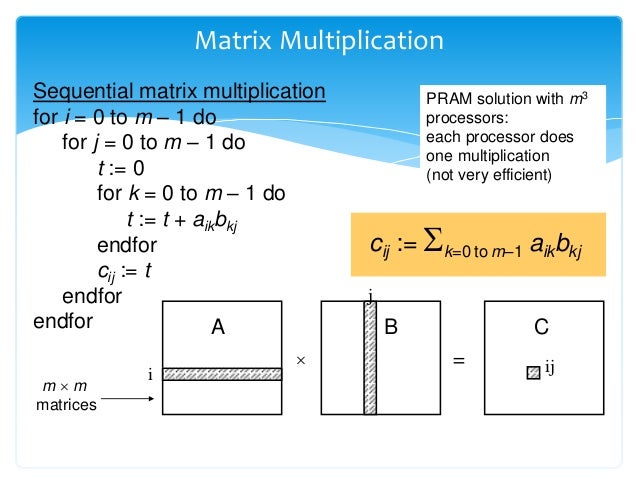
Count of multiplications for each parenthesis. We recommend the definition of supply chain management developed and used by The Global Supply Chain Forum. Using Naïve method two matrices X and Y can be multiplied if the order of these matrices are p q and q r.

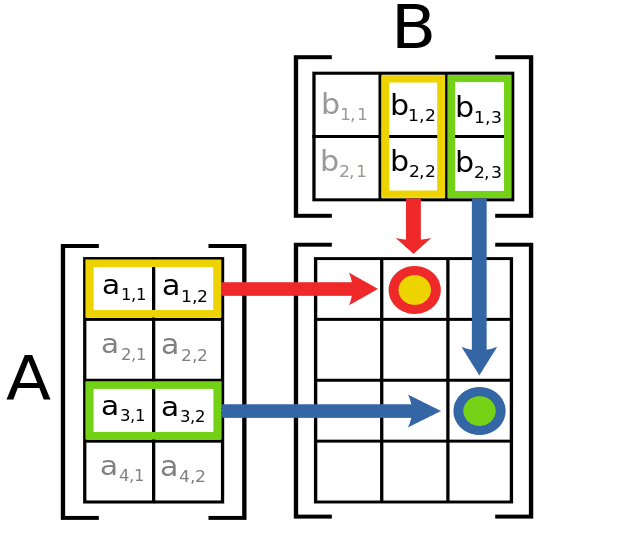
Matrix Multiplication Defined page 2 of 3 Just as with adding matrices the sizes of the matrices matter when we are multiplying. Place parenthesis at different places between. Build a matrix.

The matrices have size 4 x 10 10 x 3 3 x 12 12 x 20 20 x 7. Rec-Matrix-Chainarray p int i int j if i j mi i 0. For matrix multiplication to work the columns of the second matrix have to have the same number of entries as do the rows of the first matrix.

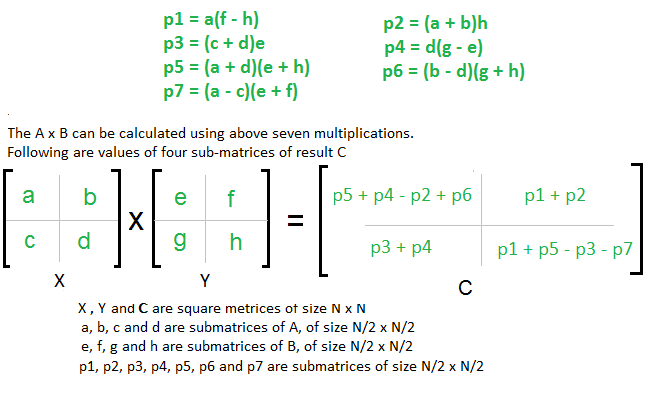
Divide a matrix of order of 22 recursively till we get the matrix of 22. A e b g a f b h c e d g c f d h. There are some procedures.

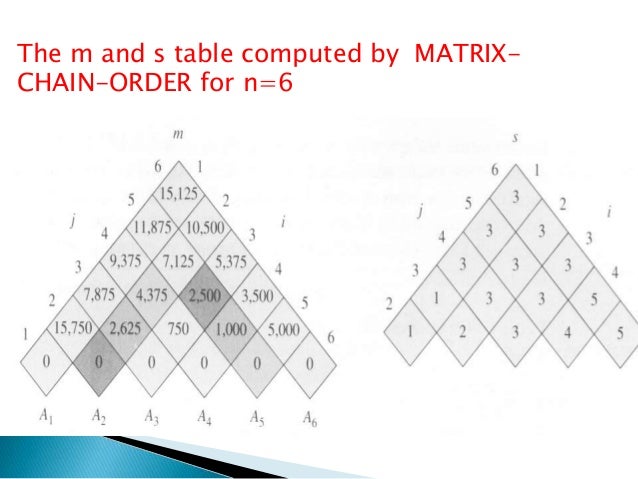
We are given the sequence 4 10 3 12 20 and 7. Following is the algorithm. Use the previous set of formulas to carry out 22 matrix multiplication.

Consider a matrix A of order 23 and another matrix B of order 32 in this case the A x B is possible because number of rows of A number of columns of B. Function OptimalMatrixChainParenthesischain n lengthchain for i 1 n mii 0 Since it takes no calculations to multiply one matrix for len 2 n for i 1 n - len 1 j i len -1 mij infinity So that the first calculation updates for k i j-1 q mi k mk1 j if q mi j The new order of parentheses is better than what we had mi j q Update si j k Record which k to split on ie. Ae bg af bh ce dg and cf dh.

Int min IntegerMAX_VALUE. First and last matrix recursively calculate. Consider the following matrices A and B.

Here we are calculating Z X Y. The manual method of multiplication procedure involves a large number of calculations especially when it comes to higher order of matrices whereas a program in C can carry out the operations with short simple and understandable codes. Static int MatrixChainOrder int p int i int j.

We need to compute M ij 0 i j 5. We know M i i 0 for all i. The matrices have dimensions 1030 305 560.

Procedure of Strassen matrix multiplication. Supply Chain Management is the integration of key business processes from end user through. On the x axis place the main elements for developing your supply chains.

Example of Matrix Chain Multiplication. Let us proceed with working away from the diagonal. Matrix-Multiplication X Y Z for i 1 to p do for j 1 to r do Z ij 0 for k.

If using the above matrices B had had only two rows its. Addition of two matrices takes O N 2 time. Combine the result of two matrixes to find the final product or final matrix.

Out of all possible combinations the most efficient way is A BCD. 2 Calculate following values recursively. Matrix C aebg afbh cedg cfdh.

We compute the optimal solution for the product of. Intuitively the multivariate chain rule mirrors the single-variable one and as well soon see the latter is just a special case of the former with derivatives replaced by derivative matrices. Placement and return the minimum count.

Introduction To Matrices And Matrix Arithmetic For Machine Learning