Skew Symmetric Matrices Properties
Matrix is called a skew symmetric matrix if T A A. X ij -x ji for all values of i and j.
Solved A Skew Symmetric Matrix A Has The Property That A Chegg Com
In other words a square matrix Q which is equal to negative of its transpose is known as skew-symmetric matrix ie.

Skew symmetric matrices properties. In other words we can say that matrix P is said to be skew-symmetric if the transpose of matrix A is equal to the negative of Matrix A ie A. Since for any matrix A kA kA it follows that 1 2 AA is a symmetric matrix and 1 2 A A is a skew-symmetric matrix. Properties Examples.
Thus any square matrix can be expressed as the sum of a symmetric and a skew-symmetric matrix. Property 1 is true only when there are no singularities present in the formulation. Q T -Q.
When we add two skew-symmetric matrices then the resultant matrix is also skew-symmetric. The symmetric matrix should be a square matrix. Obviously C is a skew-symmetric conference matrix if and only if H is skew.
Scalar product of skew-symmetric matrix is also a skew-symmetric matrix. The conference matrices constructed in Theorem 57 are skew. Yes and moreover for any n n skew-symmetric matrix A with n odd I n A is non-singular.
It is conjectured that skew Hadamard matrices exist for n 1 n 2 and all n divisible by 4. This is because the eigenvalues of A are 0 or purely imaginary coming in pairs of the form λ i for λ R. Properties of Symmetric and Skew-Symmetric Matrices There are some rules that come from the concept of Symmetric and Skew-Symmetric Matrices 1.
Hence I n A has eigenvalues 1 and 1 λ i. The matrix inverse is equal to. Every square matrix is the sum in a unique way of a symmetric and a skew-symmetric matrix.
Where aij aji for 1 i n and 1 j n. Identity matrix linear algebra matrix nonsingular matrix singular matrix skew-symmetric matrix subspace subspace criteria symmetric matrix transpose transpose matrix vector space Next story A Group Homomorphism is Injective if and only if the Kernel is Trivial. Let A be a real skew symmetric matrices of order n.
The diagonal of skew symmetric matrix consists of zero elements and therefore the sum of elements in the main diagonals is equal to zero. 7 Problems and Solutions on skew-symmetric Hermitian symmetric matrices. If the matrix is invertible then the inverse matrix is a symmetric matrix.
A matrix is skew-symmetric if and only if it is the opposite of its transpose. A 3 6 1. U v 2 4 u 2v 3 u 3v 2 u 3v 1 u 1v 3 u 1v 2 u 2v 1 3 5 1 Fromtheequalityaboveonecanseethatthefollowingskewsymmetricmatrix u 2 4 0 u 3 u 2 u 3 0 u 1 u 2 u 1 0 3 5 2 satisfiesu v u v.
Let a square matrix A of size n x n is said to be skew-symmetric if. All main diagonal entries of a skew-symmetric matrix are zero. In this video I explained class 12 Math chapter 3 matrices symmetric matrices skew symmetric matrices theoremsMπKstudyMithileshsymmetricMatrixskewSymm.
Advanced Math questions and answers. The skew-symmetric property The matrix M q - 2Cq q is skew-symmetric. Skew symmetric matrix is a square matrix Q x ij in which i j th element is negative of the j i th element ie.
A Hadamard matrix H is called skew if its entries on the main diagonal are 1 and CH I n is skew symmetric. Some of the symmetric matrix properties are given below. All entries above the main diagonal of a symmetric matrix are reflected into equal entries below the diagonal.
A matrix is called skew-symmetric if the transpose is equal to its negative. You can download Matrices Cheat Sheet by clicking on the download button below Solved Examples for You. Transposing matrices A B and C show that they are antisymmetric or skew symmetric because the transposed matrices are equivalent to their respective original matrices with the sign changed.
Form of an antisymmetric matrix. 1 Properties of skew symmetric matrices 1. Find the determinant of the following matrices by using properties of determinants and decide with reasons if they are invertible or not.
Properties of Skew Symmetric Matrix. Model setup for a robot mounted on a vehicle with coordinate frame b and inertial reference frame 0. The eigenvalue of the symmetric matrix should be a real number.
Themappingu u isbyinspectionlinearandinvertible. If for a matrix the transposed form of that matrix is the same as the negative of the original matrix then that matrix is said to be a Skew-Symmetric Matrix. Answer to Let A be a real skew symmetric matrices of order n.

Mathematics Symmetric Skew Symmetric And Orthogonal Matrix Youtube

Solved Properties Of Skew Symmetric Matrices Show That Th Chegg Com

What Is The Determinant Of Every Skew Symmetric Matrix Quora

Symmetric Matrix And Skew Symmetric Matrix Properties Of Symmetric Matrix Flexiprep

Symmetric Skew Symmetric Matrices Definition With Examples

Linear Algebra 91 Skew Symmetric Proofs Youtube

Skew Symmetric Matrices Lesson Robot Academy

Derivative Of A Rotation Matrix Robot Academy

Symmetric And Skew Symmetric Ppt Video Online Download

Symmetric And Skew Symmetric Matrices Definition Theorem Solved Example Problems
What Is A Skew Symmetric Matrix Quora

Symmetric And Skew Symmetric Matrices Lecture 6 Youtube
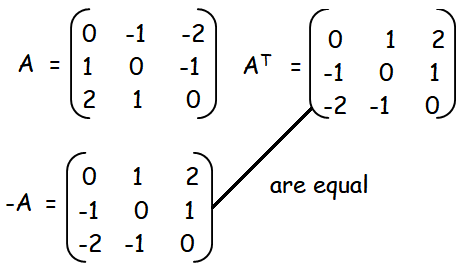
Questions On Symmetric And Skew Symmetric Matrix

Symmetric And Skew Symmetric Ppt Video Online Download
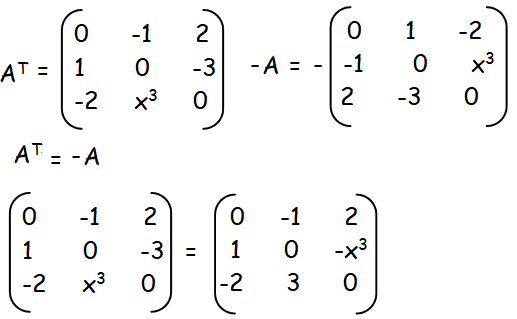
Example For Skew Symmetric Matrix

Class 12 Symmetric And Skew Symmetric Matrices Youtube

Derivative Of A Rotation Matrix Robot Academy

