Matrix Chain Multiplication Algorithm With Dynamic Programming Example

M1 N-1will be the solution to the matrix chain multiplication problem. Step2 for i in range 1 to N-1.

Matrix Chain Multiplication In C Codespeedy

If cost mi j then update if better mi j cost.

Matrix chain multiplication algorithm with dynamic programming example. In our case Mijrepresent the minimum cost to multiply a chain of matrices from matrix ito matrix j. Mii 0 Loop from chain. Return mi j.

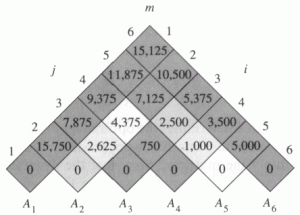
Below are the five possible parenthesizations of these arrays along with the number of multiplications. Return Fn Build from the bottom up Running Time n Very fast in practice - just need an array of linear size to store the Fi values. Given the matrices A_1 A_2 A_3 A_4.

Fi Fi -1Fi -2 5. Compute the value of an optimal solution in a bottom-up fashion. In the Chain Matrix Multiplication Problem the fundamental choice is which smaller parts of the chain to calculate first before combining them together.

Result minresultmultiplyfromiter multiplyiter1to dfrom-1diterdto. Like other typical Dynamic ProgrammingDP problems recomputations of same subproblems can be avoided by constructing a temporary array m in bottom up manner. Lects 12 and 13 slide 5.

With this representation we can safely say that Miiis 0 as there is no cost to multiply only one matrix. ABC 20 x 40 x 2 20 x 2 x 60 2 400. Intuitively the reason is this.

The important point is that when we use the equation to calculate we must have already evaluated and For both cases the corresponding length of the matrix-chain are both less than. We know M i i 0 for all i. We compute the optimal solution for the product of 2 matrices.

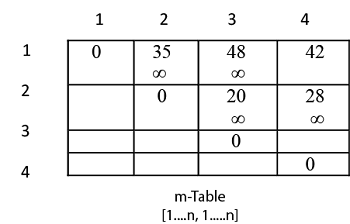
Algorithm For Matrix Chain Multiplication Step1 Create a dp matrix and set all values with a big valueINFINITY. F1 1 3. N length p-1 Where n is the total number of elements And length p 5 n 5 - 1 4 n 4 Now we construct two tables m and s.

Tn nX 1 k1 Tk Tn k O1 2 nX 1 k1 Tk On 2 Tn 1 2 2 Tn 2 2 2 2. Let us proceed with working away from the diagonal. Assume the dimensions of A_1d_0times d_1 etc.

Return final cost Like the dynamic programming algorithm this version runs in time Οn 3. Mr 0 N 1 Multiplications needed for a single matrix is 0 for i in range 1 N 1. Matrix-chain-multiply A S i j 1if j i 2 then X matrix-chain-multiply A S i S i j 3 Y matrix-chain-multiply A S S i j 1 j 4 1return matrix-multiply X Y 5 else return Ai MCM1 6 XMCM1 S164 YMCM5 6 XMCM1 S141 YMCM2 4 A1 XMCM2 S242 YMCM3 4 A2.

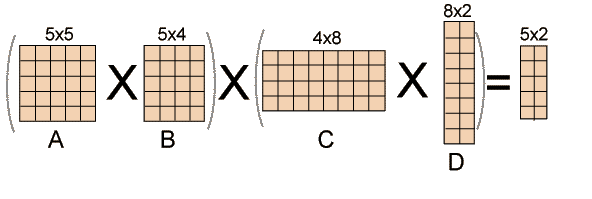
Start with for loop with L2. Update the result every time. Matrix Multiplication Let A be an n x m matrix B an m x p matrix The product of A and B is n x p matrix AB whose ij-th entry is k1 m a ik b kj In other words we multiply the entries of the i-th row of A with the entries of the j-th column of B and add them up.

C is a 2 60 matrix then. Length of array P number of elements in P length p 5 From step 3 Follow the steps in Algorithm in Sequence According to Step 1 of Algorithm Matrix-Chain-Order. A BC 40 x 2 x 60 20 x 40 x 60 48 000 operations.

When we see the subroblem for the first time we compute its solution and store in the table. Int iterresult INT_MAX. Only defined for.

Fibonacci Example contd Dynamic Programming Approach Algorithm Dyn-Fibn 1. In this video on dynamic programming I have discussed about matrix chain multiplication problem which is based upon dynamic programmingPractice questions. Below function computes the minimum number of multiplications needed to find the product of the chain of matrices in bottom up fashion def ChainMultiplication p.

For i 2 to n do 4. Max_val 99999999 Number of matrices N lenp -1 We want to return M1N as the optimal cost of product of multiplying 1N matrices M 0 N 1 for r in range N 1. The matrices have size 4 x 10 10 x 3 3 x 12 12 x 20 20 x 7.

Cost Mem-Matrix-Chainp i k Mem-Matrix-Chainp k 1 j pi 1 pk pj. F0 0 2. We need to compute M ij 0 i j 5.

We put the paranthesis at every possible step and we take the one for which computation. We are given the sequence 4 10 3 12 20 and 7. So Matrix Chain Multiplication problem has both properties see this and this of a dynamic programming problem.

Developing a Dynamic Programming Algorithm Step 3. D_0d_1d_2 d_2d_3d_4 d_0d_2d_4. A is a 20 40 matrix B is a 40 2 matrix and.

Example of Matrix Chain Multiplication. 2n Exponential is. Step3 for i in range 2 to N-1.

Matrix-chainij IF i j THEN return 0 m 1 FOR k i TO j 1 DO q Matrix-chainik Matrix-chaink 1j p i 1 p k p j IF q m THEN m q OD Return m END Matrix-chain Return Matrix-chain1n Running time.

Matrix Chain Multiplication

Matrix Chain Multiplication Dp 8 Tutorialspoint Dev

Matrix Chain Multiplication

Matrix Chain Multiplication Explained Kilichbek Haydarov

Dynamic Programming Sample Problem Matrix Chain Multiplication Review Ics 311

Matrix Chain Multiplication Different Recursive Definition Stack Overflow

Matrix Chain Multiplication Matrix Chain Multiplication Is An By Vaibhavi Maradiya Medium

Matrix Chain Multiplication Problem Using Dynamic Programming Part 2 Youtube

How To Solve Matrix Chain Multiplication Using Dynamic Programming Algorithms Blockchain And Cloud

Matrix Chain Multiplication Algorithm Javatpoint

Dynamic Programming Lecture 8 1 Dynamic Programming History

Matrix Chain Multiplication Dynamic Programming Youtube

Matrix Chain Multiplication With C Program Example Random Access Memories

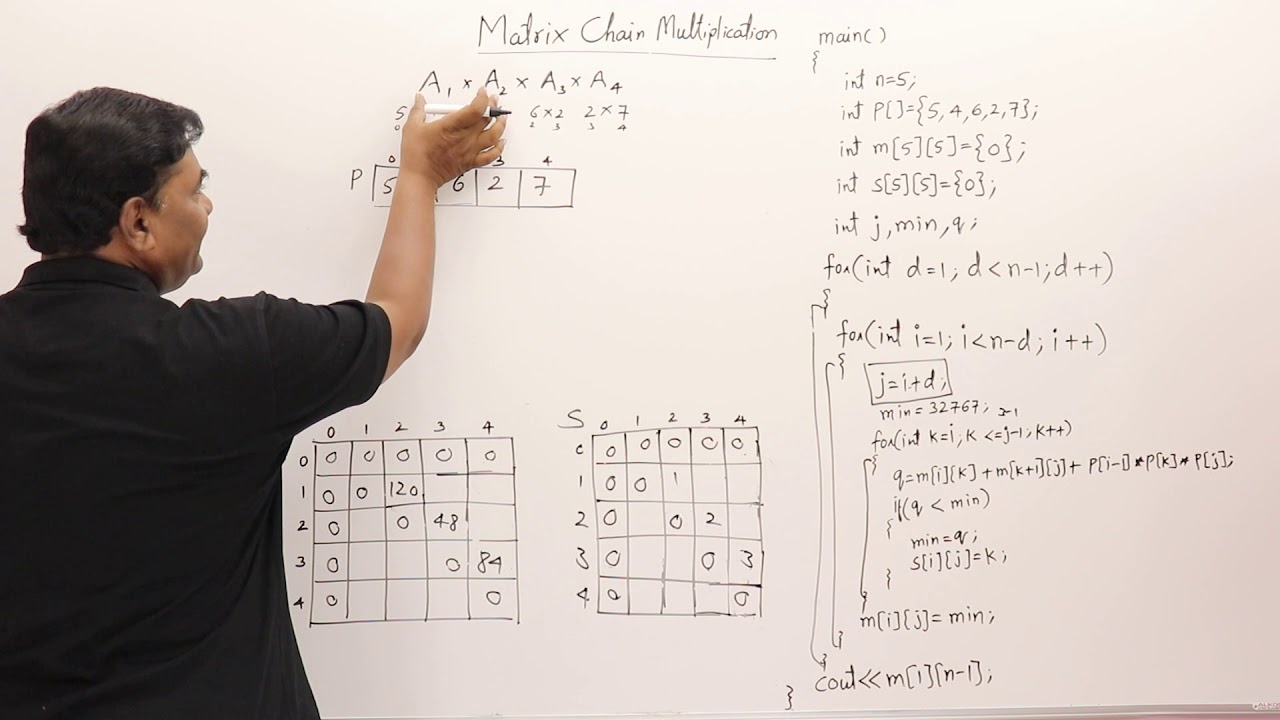
4 3 1 Matrix Chain Multiplication Program Dynamic Programming Youtube

Dynamic Programming 3 Example Matrix Chain Multiplication N N What If We Want To Multiply A String Of More Than Two Matrices Together Matrix Course Hero

Matrix Chain Multiplication

Dynamic Programming Matrix Chain Multiplication Optimal Triangulation Csc 252 Algorithms Haniya Aslam Slideshow And Powerpoint Viewer Presentation Overview Understanding Dynamic Programmin

Matrix Chain Multiplication Problem Using Dynamic Programming Part 1 Youtube

4 3 Matrix Chain Multiplication Dynamic Programming Youtube