Strassen's Matrix Multiplication Code In Python

29 Apr, 2021

For int i 0. P4 a22 b21-b11 p4 strassena22 sub_mb21b11 q2 instead.

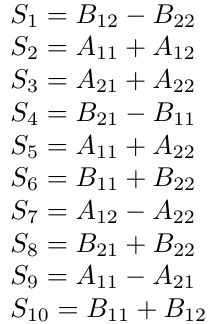
Strassen S Algorithm For Matrix Multiplication By Esha Wang Human In A Machine World Medium

The idea is similar to the Karatsuba algorithm for simple multiplication.

Strassen's matrix multiplication code in python. We can treat each element as a row of the matrix. For line in lines. T n Θ1 if n 1 8T n 2 Θn2 if n 1 T n Θ 1 if n 1 8 T n 2 Θ n 2 if n 1.

X0201 printmatrix x is for i in rangelenx. Basically you make a tradeof. For line in matrix.

As x y i new lld adjL. The first row can be selected as X 0. Int main.

Printf Enter the 4 elements of first matrix. As x y new lld adjN. Algorithm for Strassens matrix multiplication.

Instead of one multiplication you use many additions. Create a new thread to compute. Else use Strassens algorithm.

For k in range n. Fori0i. Strassens Matrix Multiplication Algorithm From the previous diagram P1 A11 A22B11 B22 P2 A21 A22 B11 P3 A11 B12 B22 P4 A22 B21 B11 P5 A11 A12 B22 P6 A21 A11 B11 B12 P7 A12 A22 B21 B22.

N len A C 0 for i in range n for j in range n for i in range n. The Strassen algorithm has a time complexity of Onlog27o1 On2807 O n l o g 2 7 o 1 O n 2807. Else Partition a into four sub matrices a11 a12 a21 a22.

Algorithm Strassenn a b d begin If n threshold then compute C a b is a conventional matrix. C ij A ik B kj return C. The above strategy is the basic O N3 strategy.

From the Case 1 of Masters Theorem the time complexity of the above approach is Onlog28 O n log 2. Int a 2 2b 2 2c 2 2ij. In Python we can implement a matrix as nested list list inside a list.

Def add A B. For example X 1 2 4 5 3 6 would represent a 3x2 matrix. As x new lld 2.

Up to 5 cash back Find strassenalgorithmpython at Staples and shop by desired features and customer ratings. N len A. 26 26 26 26 52 52 52 52 78 78 78 78 104 104 104 104 import numpy def check.

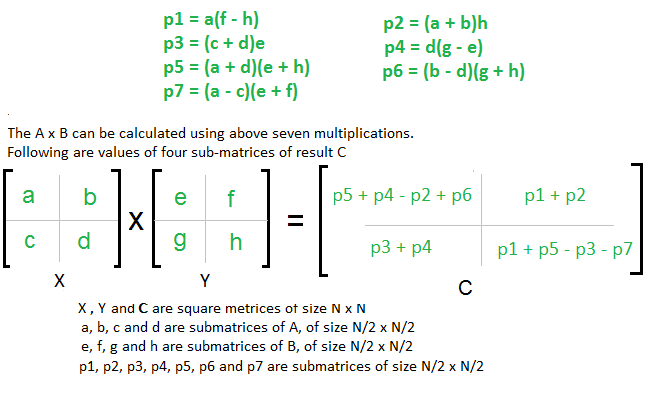
1 Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram. Mi Ai Bi. Matrix A.

For int y 0. Int adjM m 1 m. 2 Calculate following values recursively.

26 26 26 26 52 52 52 52 78 78 78 78 104 104 104 104 Should be. Using the Master Theorem with T n 8T n2 O n2 we still get a runtime of O n3. Printtxi y0034 printmatrix y is for i in rangeleny.

Strassens insight was that we dont actually need 8 recursive calls to complete this process. For each of. Strassens matrix multiplication algorithm implemented in Python.

For two 22 matrices a and b where A. Addition of two matrices takes O N 2 time. And the element in first row first column can be selected as X 0 0.

Split t else. C code of two 2 by 2 matrix multiplication using Strassen algorithm. Matrix C aebg afbh cedg cfdh.

Coding python -i strasspy Strassen Outputs. Mi i 1 to 7. Multiplication of two matrices X and Y is defined only if the number of columns in X is equal to the number of rows Y.

Print t. In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions. Partition b into four sub matrices b11 b12 b21 b22.

Compute C using the traditional matrix multiplication algorithm. 8 or On3 O n 3 which is the same as the naive method of matrix multiplication. For int j 0.

Lld As new lld 2. If the sizes of the matrices are less than the threshold. Append int el for el in line.

Divide the matrix then use the Strassens formulae. Ae bg af bh ce dg and cf dh. Join map str line def ikj_matrix_product A B.

File matrixMultpy line 106 in print strassenc d 10 File matrixMultpy line 77 in strassen p1 strassenaddMatrixa11a22 addMatrixb11b22 n2 File matrixMultpy line 78 in strassen p2 strassenaddMatrixa21a22 b11 n2 File matrixMultpy line 82 in strassen p6 strassensubMatrixa21a11 addMatrixb11b12. Traceback most recent call last. Sb01-b11 a00a01 a10a11 b10-b00 a00a11 b00b11.

For int x 0. Review Strassens sequential algorithm for matrix multiplication which requires Onlog 2 7 On281 operations. For j in range n.

Strassen algorithm is a recursive method for matrix multiplication where we divide the matrix into 4 sub-matrices of dimensions n2 x n2 in each recursive step. The algorithm is amenable to parallelizable4 A variant of Strassens sequential algorithm was developed by Coppersmith and Winograd they achieved a run time of On23753.

Strassen Matrix Multiplication Programmer Sought

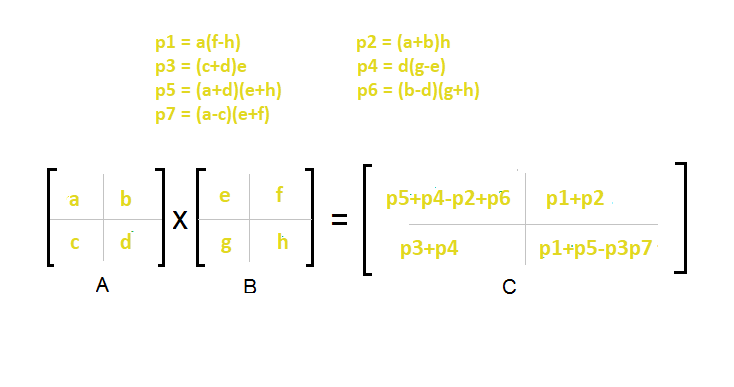
Strassen S Matrix Multiplication Algorithm

Python Implementation Of Strassen Matrix Multiplication Programmer Sought

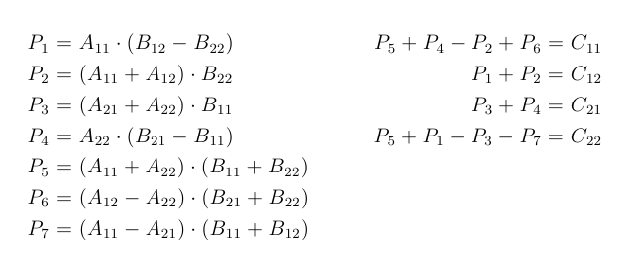
Strassen Matrix Multiplication C The Startup

Use By A Large Number Of Enterprises And Users Angular Is A Platform For Building Responsive Universal Single P App Development Process Writing Code Script Tag

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

C Program For Matrix Chain Multiplication Code Blah

Implement Strassen S Matrix Multiplication Algorithm Goeduhub Technologies

Github Rangelak Strassen Matrix Multiplication Strassen Matrix Multiplication Algorithm In C March 2017 Rangel Milushev

Strassen S Matrix Multiplication Divide And Conquer Geeksforgeeks Youtube

Python Implementation Of Strassen Matrix Multiplication Programmer Sought

2 9 Strassens Matrix Multiplication Youtube

Algorithm Divide And Conquer And Recursion Three Kinds Of Matrix Multiplication Brute Force Method Naive Divide And Conquer Method Strassen Method Programmer Sought