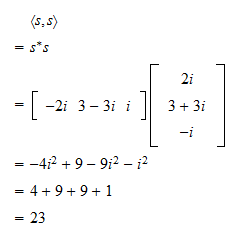Inner Product Matrix Transpose
De ne the length or norm of vby the formula kvk p hvvi q v2 1 v2n. Ie AT ij A ji ij.
Transpose Of A Matrix Product Video Khan Academy
A suo matrix is symmetric if A A which implies ay A square matrix is diagonal if the only.
Inner product matrix transpose. The geometry is in the the inner product say on R n. Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. That is the beauty of having properties like associative.
Transposes and Matrix Products. Properties of Inner and Outer Product uTv truvT. The transpose of an m nmatrix Ais the n mmatrix AT whose columns are the rows of A.
Definition of an inner and outer product of two column vectorsJoin me on Coursera. The transpose satisfies this relation using the Euclidean inner product yxsum_i x_i y_i. From now on vectors v 2Rn will be regarded as columns ie.
Hvwi v 1w 1 v nw n. We have the following properties for the inner product. A x A x x A t A x.
If u and v are column vectors of any size then uvT is the outer product of u and v. It might be hard to believe at times but math really does try to. For orthonormal matrices multiplying by the.
If U is a subspace of an inner product space V then the only vector common to both U and U is the zero vector. Recall that the transpose of a matrix is de ned by AT ij A ji. To prove this suppose that Ais n k and Bis k m.
For example if A 6 1 0 1 2 4. If a is a kx I vector then is low vector A matrix is square if R r. Then AT 0 6 1 1 2 0 4 1 A.
Transpose Dot Product Def. Are column vector and - jr are row vector The transpose of a matrix denoted B A is obtained by Hipping the matrix on its diagonal 1191 Thus buy for all and y. See this answer for a geometric description of the transpose.
Note that eai eai Just as for inner products the length of a vector u. If A 1 2 3 4 5 6 then AT 2 4 1 4 2 5 3 6 3 5. It is my understanding that the Outer Product of a vector with its transpose is symmetric in value.
Does Numpy take this into account to only do the multiplications for the upper triangle part of the output or does it calculate the whole output matrix even though it is symmetric. Numpy Performance - Outer Product of a vector with its transpose. Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A.
Note that we can de ne hvwifor the vector space kn where kis any eld but kvkonly makes sense for k R. AB is just a matrix so we can use the rule we developed for the transpose of the product to two matrices to get ABCT CT ABT CT BT AT. So for example in C C02π hektietii Z 2π 0 ektieti dt Z 2π 0 ekti dt ekti ki i 2π 0 0 if 6 k.
The columns of AT are the rows of A. In other words to nd AT you switch the row and column indexing. In other words AT undoes the action of A ie they are inverses.
Note that if Aisk xr then A is rxk. If S is a spanning set for a subspace U of ℝ n considered as column matrices and if a matrix A is created so that each row of A is the transpose of the vectors in S then U ker A. 1 Inner Product definition X Y x1.
Inner and Outer Product If u and v are column vectors with the same size then uTv is the inner product of u and v. If you have an inner product cdotcdot the adjoint of A is defined as the linear operator that satisfies the property yAx A daggeryx. 1 Real inner products Let v v 1v n and w w 1w n 2Rn.
Orthogonal matrices satisfy x y A x A y they preserve the geometry. Yn SUM_i1n xi yi x1 y1 x2 y2. We can define a Hermitian inner product on C Cab by huvi R b a utvtdt.
The Answer 1 88 people think this answer is useful. Xn yn. If you can multiply together two matrices Aand B then ABT AT BT.
Yn x1. Property of the conjugate transpose matrix with inner product 1 answer Closed 3 years ago. The rows of AT are the columns of A.
In one of the proofs in class there was given the equality for the dot product. For a matrix A the transpose is a special case of an adjoint A dagger. Matrix transpose If A rotates w by θ A cosθsinθ sinθcosθ then A1 AT rotates w 0 by θ AT cosθsinθ sinθ cosθ.
We de ne the inner product or dot product or scalar product of v and w by the following formula. Transpose and Trace Inner and Outer Product Inner and Outer Product Definition. The transpose satisfies A x y x A t y.
AAT h cos2 θsin2 θ cosθsinθsinθcosθ cosθsinθsinθcosθ cos2 θsin2 θ i 1 0 0 1.
If The Inner Product Of Two Matrices Is Zero What Does That Mean
Beyond Vectors Hungyi Lee Introduction Many Things Can
Pin On Matlab Nerd Board
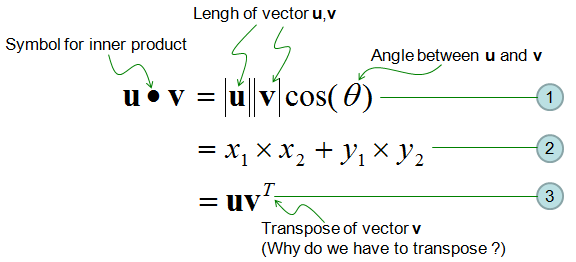
Vector Inner Product Sharetechnote
When A Moves From One Side Of The Dot Product To The Other It Becomes A T Mathematics Stack Exchange
Matrix Algebra
Microsoft Mathematics 4 0 Microsoft Mathematics Incluye Una Calculadora Grafica Que Representa Graf Ecuaciones Resolucion De Ecuaciones Calculadora Grafica
Inner Dot Product Of Two Vectors Applications In Machine Learning
Example Of Inner Product As Matrix Multiplication Mathematics Stack Exchange
Stochastic Calculus A Practical Introduction Durrett Studying Math Advanced Mathematics Logic Math
Introduction To Linear Algebra Ppt Download
Matrix Algebra
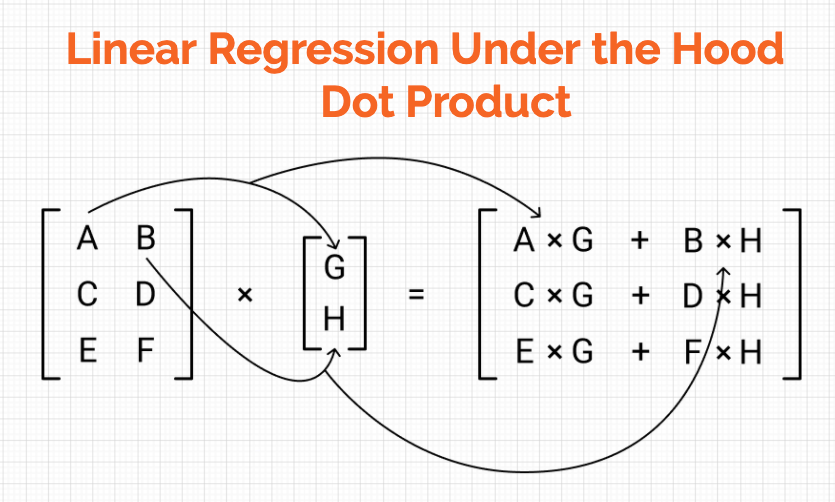
Dot Product In Linear Algebra For Data Science Using Python By Harshit Tyagi Towards Data Science
Thanksci Vi Gauge Symmetries Classical Physics Wave Function Mechanical Wave
Slide View 15 462 662 Fall 2020
Inner Product
Pin On Math
Pin On Algebra
Pin On Math
