Eigenvalues Of A Matrix Multiplied By Its Transpose
I tried to find the eigenvalues of a matrix multiplied by its transpose but I couldnt do it using numpy. Definition 3 A real matrix Q is an orthogonal matrix if the inverse of Q equals to the transpose of Q.
Testmatrix numpyarray 12 34 56 78 prod testmatrix testmatrixT print eig prod I expected to get the following result for the product.

Eigenvalues of a matrix multiplied by its transpose. Thus the eigenvalues of are Those of the inverse are and those of are. Therefore the eigenvalues of are Transposition does not change the eigenvalues and multiplication by doubles them. Ie AT ij A ji ij.
Solving this equation we find that the eigenvalues are λ1 5 λ2 10 and λ3 10. And then the transpose so the eigenvectors are now rows in Q transpose. Notice that 10 is a root of multiplicity two due to λ2 20λ 100 λ 102 Therefore λ2 10 is an eigenvalue of multiplicity two.
The result is the following equation. Is a diagonal matrix. Since is triangular its eigenvalues are equal to its diagonal entries.
Conversely if λ is an eigenvalue of α A with eigenvector v then we have that α 1 v is an eigenvector relative to λ for α 1 α A A. Those are the lambdas. The conjugate transpose of a matrix with real entries reduces to the transpose of as the conjugate of a real number is the number itself.
Motivation edit The conjugate transpose can be motivated by noting that complex numbers can be usefully represented by 22 real matrices obeying matrix addition and multiplication. If the scalar is 0 then α A is the zero matrix having only the zero eigenvalue. λ 5λ2 20λ 100 0.
Consider the characteristic polynomial of AT. Yeah thats called the spectral theorem. Definition 1 A real matrix A is a symmetric matrix if it equals to its own transpose that is A AT.
This result is the characteristic polynomial of A soATandAhave the same characteristic polynomial and hence they have the same eigenvalues. Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. Those are the numbers lambda 1 to lambda n on the diagonal of lambda.
We say that the transform diagonalizes the matrix. This video works through an example of first finding the transpose of a 2x3 matrix then multiplying the matrix by its transpose and multiplying the transpo. Every symmetric matrix is an orthogonal matrix times a diagonal matrix times the transpose of the orthogonal matrix.
An orthogonal matrix is one whose transpose is its inverse This solves the problem because the eigenvalues of the matrix are the diagonal values in and the eigenvectors are the column vectors of. JI ATj jI ATj jI Aj since a matrixand its transpose have the same determinant. α A v α λ v λ α v This shows that α v 0 is an eigenvector relative to λ for α A.
Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. It always works for small matrices. Definition 2 A complex matrix A is a hermitian matrix if it equals to its own complex conjugate trans-pose that is A AH.
5 11 17 23 11 25 39 53 17 39 61 83 23 53 83 113. Viewed 6k times. Why does the symmetry test fails here for medium-size-random matrices.
There is a mathematical theorem stating that a matrix A multiplied with its transpose yields a symmetric positive definite matrix thus leading to positive eigenvalues. I recall being told that the eigenvalues of the matrix formed by multiplying a matrix by its transpose are the squares of the eigenvalues of the original matrix. So with a scalar α 0 the eigenvalues are multiplied by α but the eigenvectors dont change.

Linear Algebra 17g Easy Eigenvalues The Transpose Youtube

True Or False A The Eigenvectors And Eigenvalues Of Chegg Com

Eigenvalues And Eigenvectors In Matlab Youtube

Ch8 Pr13 Eigenvalues Of A Matrix And Its Transpose Youtube

Matrix Multiplication And Associated Properties Youtube
Https Www Seas Upenn Edu Cis520 Papers Bishop Appendix C Pdf
The Singular Value Decomposition Guzinta Math
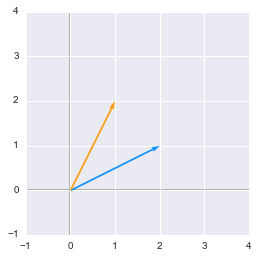
Introduction To Eigendecomposition Using Python Numpy Examples And Drawings

Eigenvalues Of A Matrix And Its Transpose Are The Same Problems In Mathematics

Eigenvalues Of A 3x3 Matrix Video Khan Academy

Mca Free Full Text Practical Sparse Matrices In C With Hybrid Storage And Template Based Expression Optimisation Html

Is An Eigenvector Of A Matrix An Eigenvector Of Its Inverse Problems In Mathematics

Linear Algebra 101 Part 9 Singular Value Decomposition Svd By Sho Nakagome Sho Jp Medium

Mathconceptions Algebra Classroom Algebra Algebra 2

Pin On Engineering Mathematics